Филтър бразда

Един филтър бразда (от англ., "notch" – "дефиле, бразда") е честотен филтър, който пропуска всички честоти с изключение на някаква много тясна лента от честоти.

Един филтър бразда по принцип е един много тесен режекторен филтър. Обратното на един филтър бразда е един филтър връх.

Примери на филтри бразда със звуково парче

Виж Orinj Филтър бразда и Orinj Филтър бразда 2 за да чуеш звукови парчета преди и след филтри бразда.

Работа с филтрите бразда

При смесването на музика, един филтър бразда може да се използва за да се махнат тесни ленти от прекалено силни честоти, които правят звука дразнещ по някакъв начин – прекалено буботещ, на нос или така нататък. Примери на такива типове еквилизация са дадени в темата Еквилайзер.

Един филтър бразда също може да се използва например за да премахне нежелания брум в електрическото оборудване при записа на музика, ако този брум се появява в записа. Честотата на променливия електрически ток обикновено е 50 Hz или 60 Hz и в този случай филтъра бразда трябва да бъде проектиран така, че да премахва съответно честотата 50 Hz или 60 Hz от сигнала. Един идеален филтър бразда ще премахне само тези честоти. Филтрите бразда на практика ще премахнат една тясна лента от честоти около тези честоти.

Пример: цифров филтър бразда с неограничен импулсен спектър

Функцията

$$H(S)=(\frac{S^2+1}{S^2+\frac{S}{Q}+1})^n$$

е нормализираната трансферна функция на един филтър бразда с неограничен импулсен спектър от разряд 2n, като 1/Q е приблизителната ширина на браздата, както е описано по-долу.

Да предположим, че искаме да изчислим параметрите на един филтър бразда с неограничен импулсен спектър, с разряд 2 и с честота на браздата ω_c (ω_c е ъгловата честота, която филтърът трябва да премахне, и е между 0 и π). Можем да заместим S = s / ω_c (където s = jω) и n = 1 и да използваме билинейното преобразуване s = 2 (z – 1) / (z + 1). Трансферната функция на филтъра бразда от разряд 2 е

$$H(z)=\frac{(4+\omega_c^2)+(2\omega_c^2-8)z^{-1}+(4+\omega_c^2)z^{-2}}{(4+\frac{\omega_c}{Q}+\omega_c^2)+(2\omega_c^2-8)z^{-1}+(4-\frac{\omega_c}{Q}+\omega_c^2)z^{-2}}$$

Да предположим, че искаме бразда при ω_c = 0.6 с ширина 1/Q = 0.5 (по принцип, браздата ще бъде при ω_c = 2 arctan(0.6/2) ≈ 0.583, заради изкривяването на честотния диапазон от билинейното преобразуване). Трансферната функция на филтъра бразда от втори разряд ще стане

$$H(z)=\frac{0.935622-1562232\,z^{-1}+0.935622\,z^{-2}}{1-1562232\,z^{-1}+0.871245\,z^{-2}}$$

Самият филтър се дава от формулата

$$y(k) = 0.935622 x(k) – 1.562232 x(k-1) + 0.935622 x(k-2) + 1.562232 y(k-1) – 0.871245 y(k-2)$$

където x(k) и y(k) са съответно входния сигнал и изходния сигнал при проба k.

Ако предположим, че пробната честота е 2000 Hz, тогава амплитудният спектър на примерния филтър бразда от втори разряд ще е следната.

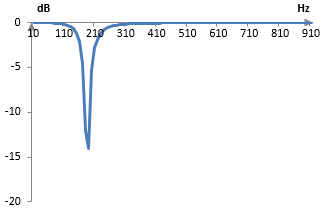
Този филтър пропуска всички честоти с изключение на една тясна лента от честоти ("браздата"). Честотата на самата бразда, след като пробната честота е 2000 Hz, е ω_c = (0.6 * 2000) / (2 π) = 191 Hz. Ширината на браздата е около 1/Q = (0.5 * 2000) / (2 π) = 159 Hz.

Характеристики на филтрите бразда

Филтърът бразда по-горе е само един пример и има различни начини да се създадат цифрови или аналогови филтри бразда, които могат да имат различни характеристики. Филтрите бразда обикновено се характеризират със ширината и дълбочината на браздата в техния амплитуден спектър. Ширината на браздата във филтъра в примера по-горе е около 160 Hz и нейната дълбочина е около -14 dB. При този определен филтър, една бразда с по-голяма дълбочина ще има и по-голяма ширина.

Един филтър бразда може да бъде проектиран така, че да премахва не само една определена честота, а и хармоници на честотата на браздата. Един филтър бразда на 60 Hz например може да бъде проектиран така, че да премахва и 120 Hz, 180 Hz, 240 Hz и така нататък.