Билинейно преобразуване

Билинейното преобразуване е заместването

$$s=\frac{2(z-1)}{z+1}$$

което се използва used за да се превърне представянето на една непрекъсната (не дискретизирана или "аналогова") система в една дискретизирана (или "цифрова") система.

Нискочестотният филтър на Филтър на от втори разряд и с преходна честота ω_c например обикновено е записан с неговата Трансферна функция с преобразуването на Лаплас

$$H(s)=\frac{\omega_c^2}{s^2+\sqrt{2}\omega_cs+\omega_c^2}$$

С билинейното преобразуване, трансферната функция на същия филтър с Преобразуване то Z е

$$H(\frac{2(z-1)}{z+1})=\frac{\omega_c^2}{(\frac{2(z-1)}{z+1})^2+\sqrt{2}\omega_c^2\frac{2(z-1)}{z+1}+\omega_c^2}$$ $$=\frac{\omega_c^2+2\omega_c^2z^{-1}+\omega_c^2z^{-2}}{(4+2\sqrt{2}\omega_c+\omega_c^2)+(-8+2\omega_c^2)z^{-1}+(4-2\sqrt{2}\omega_c+\omega_c^2)z^{-2}}$$

След като разделим всички коефициенти по първия коефициент в знаменателя, получаваме

$$H(z) = \frac{a_0+a_1z^{-1}+a_2z^{-2}}{1+b_1z^{-1}+b_2z^{-2}}$$ $$a_0=a_2=\frac{\omega_c^2}{4+2\sqrt{2}\omega_c+\omega_c^2}$$ $$a_1=\frac{2\omega_c^2}{4+2\sqrt{2}\omega_c+\omega_c^2}$$ $$b_1=\frac{-8+2\omega_c^2}{4+2\sqrt{2}\omega_c+\omega_c^2}$$ $$b_2=\frac{4-2\sqrt{2}\omega_c+\omega_c^2}{4+2\sqrt{2}\omega_c+\omega_c^2}$$

и импулсният спектър на филтъра (самото му осъществяване на практика) е

$$y(k)=a_0x(k)+a_1x(k-1)+a_2x(k-2)-b_1y(k-1)-b_2y(k-2)$$

където x(n) пробите на входния сигнал и y(n) са пробите на изходния сигнал.

Извеждане на билинейното преобразуване

Билинейното преобразуване следва от реда на Тейлър на функцията e^sT/2.

$$z=e^{sT}=\frac{1+\frac{(\frac{sT}{2})^1}{1!}+\frac{(\frac{sT}{2})^2}{2!}+...}{1+\frac{(-\frac{sT}{2})^1}{1!}+\frac{(-\frac{sT}{2})^2}{2!}+...}\approx\frac{1+\frac{sT}{2}}{1-\frac{sT}{2}}$$

Изкривяване на честотите с билинейното преобразуване

Забележи, че характеристиките на произведените филтри се оценяват при s = jω или z = e^jω. Обаче,

$$H(s)=H(j\omega)$$ $$H(\frac{2(z-1)}{z+1})=H(\frac{2(e^{j\omega}-1)}{e^{j\omega}+1})=H(2\frac{e^{\frac{j\omega}{2}}(e^{\frac{j\omega}{2}}-e^{-\frac{j\omega}{2}})}{e^{\frac{j\omega}{2}}(e^{\frac{j\omega}{2}}+e^{-\frac{j\omega}{2}})})$$ $$=H(2\frac{2jsin(\frac{\omega}{2})}{2cos(\frac{\omega}{2})})=H(2j\,tan(\frac{\omega}{2}))$$

Така, дискретизираният филтър H(z), получен след билинейното преобразуване на H(s), ще прави това при дискретизираната честота ω_d, което прави не дискретизираният филтър H(s) при честотата ω_a = 2 tan(ω_d/2). (Или пък, ω_d = 2 arctan(ω_a/2)).

Вземи например филтъра на Батъруърт по-горе. Неговият Амплитуден спектър, изчислен от H(s), е

$$|H(j\omega)H(-j\omega)|=\sqrt{\frac{\omega_c^4}{\omega^4+\omega_c^4}}$$

Амплитудният спектър на филтъра след билинейното преобразуване може да се изчисли от

$$H(z)=\frac{\omega_c^2z+2\omega_c^2+\omega_c^2z^{-1}}{(4+2\sqrt{2}\omega_c+\omega_c^2)z+(-8+2\omega_c^2)+(4-2\sqrt{2}\omega_c+\omega_c^2)z^{-1}}$$

и е

$$|H(e^{j\omega})H(e^{-j\omega})|=\sqrt{\frac{\omega_c^4(cos(\omega)+1)^2}{\omega_c^4(cos(\omega)+1)^2+16(cos(\omega)+1)^2-64cos(\omega)}}$$ $$=\sqrt{\frac{\omega_c^4}{\omega_c^4+16\frac{(cos(\omega)-1)^2}{(cos(\omega)+1)^2}}}=\sqrt{\frac{\omega_c^4}{\omega_c^4+(2tan(\frac{\omega}{2}))^4}}$$

Това изкривяване на честотния диапазон е малко за малки ω и се увеличава, когато ω се увеличава (ω е между 0 и π). At ω_a = 1, for example, ω_d ≈ 0.927.

Когато създаваме цифрови филтри, това честотно изкривяване може да се поправи по два начина. Първо, един дискретен филтър с преходната честота ω_d може да бъде създаден с билинейното преобразуване на един недискретизиран филтър с преходна честота ω_a = 2 tan(ω_d/2). Или пък, вместо билинейното преобразуване, можем да използваме биквадратното преобразуване

$$s=\frac{1}{K}\frac{z-1}{z+1}, \, K=tan(\frac{\omega_c}{2})$$

Например, филтърът шелф с нискочестотно усилване от втори разряд с преходна честота ω_c и амплитуда G

$$H(s)=\frac{s^2+\sqrt{2G}\omega_cs+G\omega_c^2}{s^2+\sqrt{2}\omega_cs+\omega_c^2}$$

може да бъде изписан след билинейното преобразуване като

$$H(z)=\frac{(4+2\sqrt{2G}\omega_c+G\omega_c^2)+(-8+2G\omega_c^2)z^{-1}+(4-2\sqrt{2G}\omega_c+G\omega_c^2)z^{-2}}{(4+2\sqrt{2}\omega_c+\omega_c^2)+(-8+2\omega_c^2)z^{-1}+(4-2\sqrt{2}\omega_c+\omega_c^2)z^{-2}}$$

или след биквадратното преобразуване като

$$H(z)=\frac{(1+\sqrt{2G}K+GK^2)+(-2+2GK^2)z^{-1}+(1-\sqrt{2G}K+GK^2)z^{-2}}{(1+\sqrt{2}K+K^2)+(-2+2K^2)z^{-1}+(1-\sqrt{2}K+K^2)z^{-2}}$$

Съответните амплитудни спектри при примерната преходна честота ω_c = 2 и в двата случая, K = tan(ω_c / 2), пробна честота 2000 Hz и допълнителна амплитуда G = 2 (≈ 6 dB) са следните.

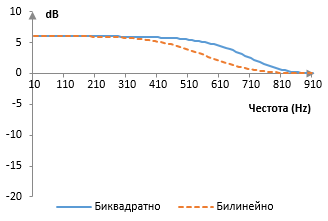
Стабилността на филтрите и билинейното преобразуване

Забележи, че при s = σ + j ω, ако Re(s) = σ < 0, тогава

$$|z|=|\frac{2+s}{2-s}|=|\frac{2+\sigma+j\omega}{2+\sigma-j\omega}|=\frac{|2+\sigma+j\omega|}{|2-\sigma-j\omega|}$$ $$=\frac{\sqrt{(2+\sigma)^2+\omega^2}}{\sqrt{(2-\sigma)^2+\omega^2}}\lt1$$

Така, ако имаме една трансферна функция с преобразуването на Лаплас на един стабилен филтър с корени на знаменателя в лявата част на комплексната s- равнина, трансферната функция, която ще получим с билинейното преобразуване ще има корени, които са в кръга с радиус единица и филтърът ще бъде стабилен. Билинейното преобразуване запазва стабилността.