The Kaiser-Bessel window coefficients are given by the following formula
$$a(k)=0.402-0.498 \, \cos(\frac{2\pi k}{N-1})+0.098 \, \cos(\frac{4\pi k}{N-1})-0.001 \, \cos(\frac{6\pi k}{N-1})$$
where N is the length of the filter and k = 0, 1, …, N – 1.
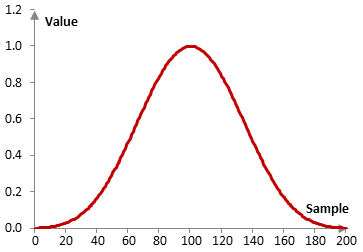
Consider a finite impulse response (FIR) low pass filter of length N = 201. The following is the Kaiser-Bessel window.
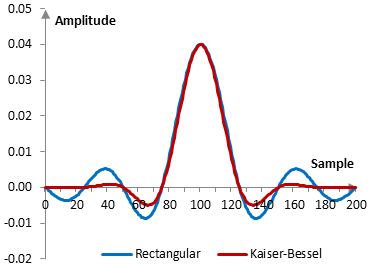
Given a sampling frequency of 2000 Hz and a filter cutoff frequency of 40 Hz, the impulse response of the filter with a rectangular window (with no window) and with the Kaiser-Bessel window is as follows.
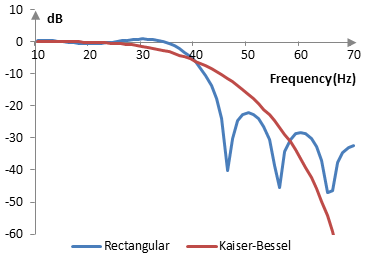
The magnitude response of the same filter is shown on the graph below.
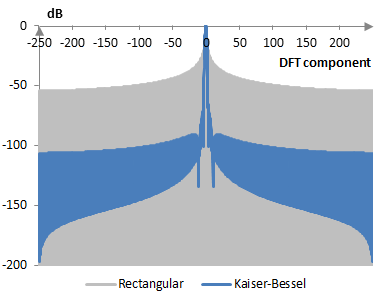
Measures for the Kaiser-Bessel window
The following is a comparison of the discrete Fourier transform of the Kaiser-Bessel window and the rectangular window.
The Kaiser-Bessel window measures are as follows.
| Coherent gain | 0.40 |
| Equivalent noise bandwidth | 1.80 |
| Processing gain | -2.55 dB |
| Scalloping loss | -1.02 dB |
| Worst case processing loss | -3.57 dB |
| Highest sidelobe level | -65.3 dB |
| Sidelobe falloff | -11.8 dB / octave, -39.3 dB / decade |
| Main lobe is -3 dB | 1.70 bins |
| Main lobe is -6 dB | 2.40 bins |
| Overlap correlation at 50% overlap | 0.072 |
| Amplitude flatness at 50% overlap | 0.608 |
| Overlap correlation at 75% overlap | 0.537 |
| Amplitude flatness at 75% overlap | 1.000 |
See also:
Window
Add new comment