The Planck-taper window coefficients are given by the following formula
$$a(k)=\begin{cases} 0, \,\,\, k=0 \\ \frac{1}{e^{z_a(k)}+1}, \,\,\, 0 \lt k \lt \epsilon (N-1) \\ 1, \,\,\, \epsilon (N-1) \le k \le (1-\epsilon)(N-1) \\ \frac{1}{e^{z_b(k)}+1}, \,\,\, (1-\epsilon)(N-1) \lt k \lt N-1 \\ 0, \,\,\, k = N-1\end{cases}$$ $$z_a(k)=\epsilon (N-1)(\frac{1}{k}+\frac{1}{k-\epsilon (N-1)})$$ $$z_b(k)=\epsilon (N-1)(\frac{1}{N-1-k}+\frac{1}{(1-\epsilon) (N-1)-k})$$ $$0 \lt \epsilon \le 0.5$$
where N is the length of the filter and k = 0, 1, …, N – 1. ε controls the size of the top portion of the window (see below), where the window is equal to 1.
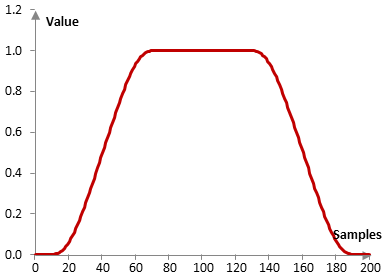
Consider a finite impulse response (FIR) low pass filter of length N = 201. The following is the Planck-taper window with ε = 0.4 .
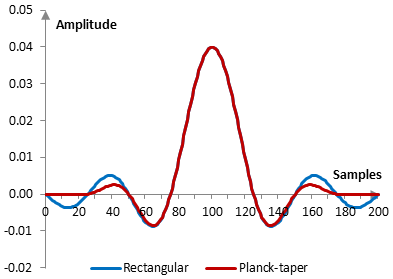
Given a sampling frequency of 2000 Hz and a filter cutoff frequency of 40 Hz, the impulse response of the filter with a rectangular window (with no window) and with the Planck-taper window is as follows.
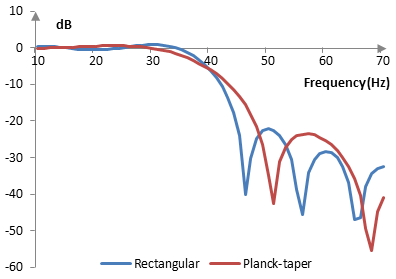
The magnitude response of the same filter is shown on the graph below.
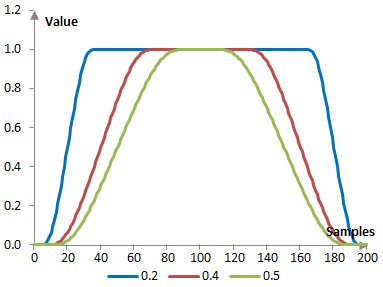
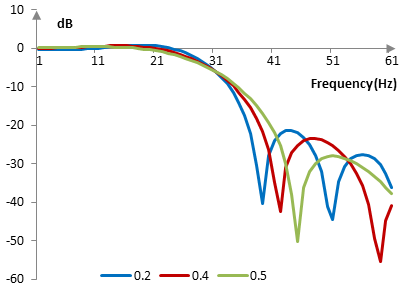
With larger ε, the top of the window becomes narrower and the transition band of the filter becomes wider, with better stop band attenuation. The following is the Planck-taper window with three different values of ε.
The following are the corresponding magnitude responses for the same filter used above.
Measures for the Planck-taper window
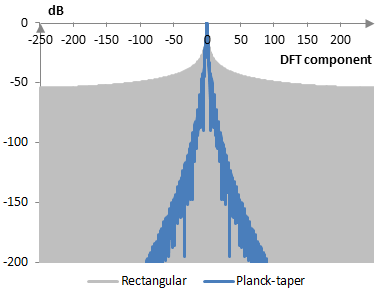
The following is a comparison of the discrete Fourier transform of the Planck-taper window (ε = 0.4) and the rectangular window.
The Planck-taper window measures are as follows.
| ε | 0.2 | 0.4 | 0.5 |
| Coherent gain | 0.80 | 0.60 | 0.50 |
| Equivalent noise bandwidth | 1.19 | 1.46 | 1.63 |
| Processing gain | -0.77 dB | -1.64 dB | -2.11 dB |
| Scalloping loss | -2.46 dB | -1.51 dB | -1.20 dB |
| Worst case processing loss | -3.22 dB | -3.15 dB | -3.31 dB |
| Highest sidelobe level | -13.9 dB | -17.5 dB | -23.2 dB |
| Sidelobe falloff | -27.4 dB / octave, -90.9 dB / decade | -30.9 dB / octave, -102.6 dB / decade | -30.8 dB / octave, -102.3 dB / decade |
| Main lobe is -3 dB | 1.10 bins | 1.40 bins | 1.56 bins |
| Main lobe is -6 dB | 1.50 bins | 1.92 bins | 2.16 bins |
| Overlap correlation at 50% overlap | 0.392 | 0.202 | 0.115 |
| Amplitude flatness at 50% overlap | 0.500 | 0.672 | 1.000 |
| Overlap correlation at 75% overlap | 0.721 | 0.666 | 0.614 |
| Amplitude flatness at 75% overlap | 0.860 | 0.923 | 1.000 |
See also:
Window
Add new comment