The triangular window coefficients are given by the following formula
$$a(k)=\frac{2}{N-1}(\frac{N-1}{2}-|k-\frac{N-1}{2}|)=1-|\frac{k-\frac{N-1}{2}}{\frac{N-1}{2}}|$$
where N is the length of the filter and k = 0, 1, …, N – 1.
Different definitions may use N / 2 or (N + 1) / 2 in the denominator of the last expression. When (N – 1) /2 is used, as in the formula above, the window is also known as the Bartlett window, or the triangular window with zero end points.
Consider a finite impulse response (FIR) low pass filter of length N = 201. The following is the triangular window.
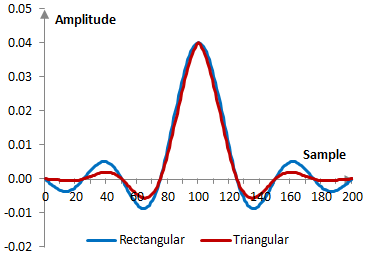
Given a sampling frequency of 2000 Hz and a filter cutoff frequency of 40 Hz, the impulse response of the filter with a rectangular window (with no window) and with the triangular window is as follows.
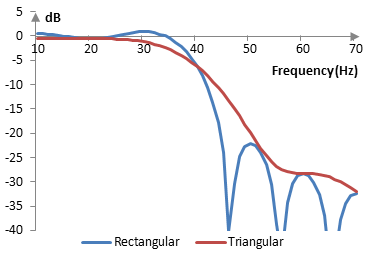
The magnitude response of the same filter is shown on the graph below.
Deriving the triangular window from the rectangular window
Take two rectangular windows f(k) and g(n) of length N.
$$f(k)=\begin{cases} 1, \,\, 0 \le k \le N-1 \\ 0, \,\, k <0, k > N-1 \end{cases}$$ $$g(k)=\begin{cases} 1, \,\, 0 \le k \le N-1 \\ 0, \,\, k <0, k > N-1 \end{cases}$$
The convolution of f(k) and g(n) is as follows.
$$(f * g)(n)=\sum_{k=-\infty}^{\infty} f(k) \, g(n-k) = \sum_{k=0}^{N-1} g(n-k)$$
The second sum above follows as f(k) is zero outside of the interval from 0 to N – 1 and 1 inside that interval.
If n < 0, the convolution is zero. If 0 ≤ n ≤ N – 1, then the sum above evaluates to n. By the fact that g = 1 only for 0 ≤ n – m ≤ N – 1, which is equivalent to n – (N – 1) ≤ m ≤ n, when n > N – 1
$$(f * g)(n)=\sum_{m=n-(N-1)}^{N-1} g(n-m) = 2(N-1)-n$$
Thus, the convolution of two rectangular windows of length N produces
$$(f * g)(n)=\begin{cases} n, \,\,\, 0 \le n \le N-1 \\ 2(N-1)-n, \,\,\, N-1 \lt n \le 2(N-1) \\ 0, \,\,\, n \lt 0 \end{cases}$$
or
$$(f * g)(n)=\begin{cases} N-1-|n-(N-1)|, \,\,\, 0 \le n \le 2(N-1) \\ 0, \,\,\, n \lt 0, n \gt 2(N-1) \end{cases}$$
This is a triangular window, which, however, is of twice the length of the rectangular windows (less 1). Replacing N – 1 with (N – 1) / 2 and scaling the window to peak at 1 produces the triangular window formula at the beginning of this topic.
Windows that are produced by the convolution of the rectangular window are known as basic spline or B-spline windows. They include the rectangular window (order 1), the triangular window (order 2), and the Parzen window (order 4), where each successive order is produced by convolving the previous order with the same rectangular window.
Measures for the triangular window
The following graph compares the discrete Fourier transform of the triangular window with that of the rectangular window.
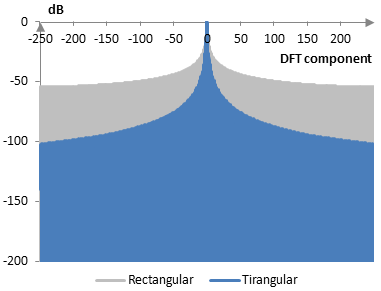
The triangular window measures are as follows.
| Coherent gain | 0.50 |
| Equivalent noise bandwidth | 1.34 |
| Processing gain | -1.26 dB |
| Scalloping loss | -1.82 dB |
| Worst case processing loss | -3.07 dB |
| Highest sidelobe level | -26.5 dB |
| Sidelobe falloff | -11.4 dB / octave, -37.7 dB / decade |
| Main lobe is -3 dB | 1.28 bins |
| Main lobe is -6 dB | 1.78 bins |
| Overlap correlation at 50% overlap | 0.248 |
| Amplitude flatness at 50% overlap | 1.000 |
| Overlap correlation at 75% overlap | 0.718 |
| Amplitude flatness at 75% overlap | 1.000 |
See also:
Window
Add new comment