Коефициентите на триъгълния прозорец се дават от формулата
$$a(k)=\frac{2}{N-1}(\frac{N-1}{2}-|k-\frac{N-1}{2}|)=1-|\frac{k-\frac{N-1}{2}}{\frac{N-1}{2}}|$$
където N е дължината на филтъра и k = 0, 1, …, N – 1.
Различни определения използват N / 2 или (N + 1) / 2 в знаменателя на последната част на формулата. Когато се използва (N – 1) /2, както във формулата по-горе, прозорецът също така се нарича и прозорец на Бартлет или триъгълен прозорец с крайни точки равни на нула.
Вземи един нискочестотен филтър с краен импулсен спектър (FIR) и с дължина N = 201. Следното е триъгълния прозорец.
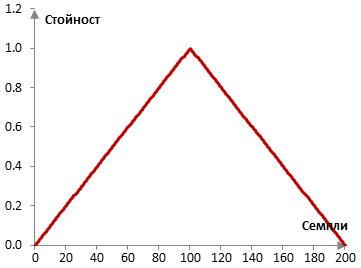
Ако пробната честота е 2000 Hz и преходната честота на филтъра е 40 Hz, тогава импулсният спектър на филтъра с правоъгълен прозорец (без прозорец) и с триъгълния прозорец е следния.
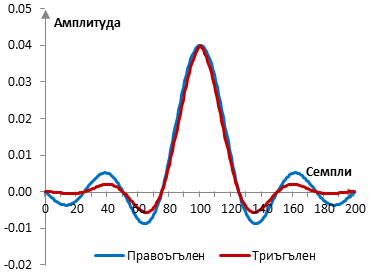
Амплитудният спектър на същия филтър е показан в следната графиката.
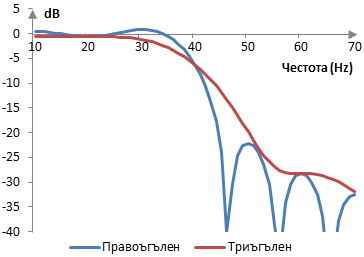
Извеждане на триъгълния прозорец от правоъгълния прозорец
Вземи два правоъгълни прозореца f(k) и g(n) с дължина N.
$$f(k)=\begin{cases} 1, \,\, 0 \le k \le N-1 \\ 0, \,\, k <0, k > N-1 \end{cases}$$ $$g(k)=\begin{cases} 1, \,\, 0 \le k \le N-1 \\ 0, \,\, k <0, k > N-1 \end{cases}$$
Конволюцията на f(k) и g(n) е следната
$$(f * g)(n)=\sum_{k=-\infty}^{\infty} f(k) \, g(n-k) = \sum_{k=0}^{N-1} g(n-k)$$
Втората сума по-горе следва от това, че f(k) е нула извън интервала от 0 до N – 1 и 1 в интервала.
Ако n < 0, конволюцията е нула. Ако 0 ≤ n ≤ N – 1, горната сума е равна на n. Поради факта, че g = 1 само при 0 ≤ n – m ≤ N – 1, което е еквивалентно на n – (N – 1) ≤ m ≤ n, когато n > N – 1
$$(f * g)(n)=\sum_{m=n-(N-1)}^{N-1} g(n-m) = 2(N-1)-n$$
Така, коволюцията на два правоъгълни прозореца с дължина N дава
$$(f * g)(n)=\begin{cases} n, \,\,\, 0 \le n \le N-1 \\ 2(N-1)-n, \,\,\, N-1 \lt n \le 2(N-1) \\ 0, \,\,\, n \lt 0 \end{cases}$$
или
$$(f * g)(n)=\begin{cases} N-1-|n-(N-1)|, \,\,\, 0 \le n \le 2(N-1) \\ 0, \,\,\, n \lt 0, n \gt 2(N-1) \end{cases}$$
Това е триъгълният прозорец, който обаче е с дължина два пъти дължината на правоъгълните прозорци (минус 1). Ако заместим N – 1 с (N – 1) / 2 и умножим по една скаларна величина за да получим прозорец с връх равен на 1, ще получим формулата за триъгълния прозорец в началото на тази тема.
Прозорците, които се получават от конволюцията на правоъгълни прозорци, се наричат прозорци на основния жлеб (от англ., "basic spline" или "B-spline"). Такива са правоъгълния прозорец (първи разряд), триъгълния прозорец (втори разряд) и прозореца на Парзън (четвърти разряд 4), където всеки следващ разряд се получава от предишния разряд с конволюция със същия правоъгълен прозорец.
Измерения за триъгълния прозорец
Следната графика сравнява дискретизираното преобразуване на Фурие на триъгълния прозорец с правоъгълния прозорец.
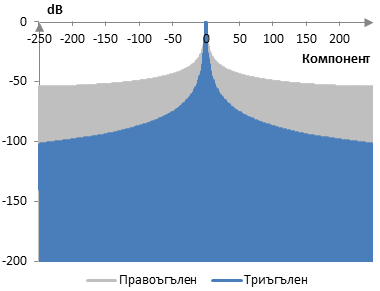
Измеренията на триъгълния прозорец са следните.
| Кохерентна амплитуда | 0.50 |
| Еквивалентна лента на шума | 1.34 |
| Загуба при преработката | -1.26 dB |
| Загуба на лоба | -1.82 dB |
| Загуба при преработката в най-лошия случай | -3.07 dB |
| Ниво на най-високия страничен лоб | -26.5 dB |
| Спадане на страничните лобове | -11.4 dB / октава, -37.7 dB / декада |
| Главният лоб е -3 dB | 1.28 компонента |
| Главният лоб е -6 dB | 1.78 компонента |
| Корелация при застъпването при застъпване от 50% | 0.248 |
| Амплитудна гладкост при застъпване от 50% | 1.000 |
| Корелация при застъпването при застъпване от 75% | 0.718 |
| Амплитудна гладкост при застъпване от 75% | 1.000 |
Виж също:
Прозорец
Добави нов коментар