The Tukey window coefficients are given by the following formula
$$a(k)=\begin{cases} 0.5 (1+\cos(\frac{\pi(|k-M|-\alpha M)}{(1-\alpha)M})), \,\,\, |k-M| \ge \alpha M \\ 1, \,\,\, |k-M| \lt \alpha M \end{cases}$$
where N is the length of the filter, M = (N – 1) / 2, k = 0, 1, …, N – 1, and α is a constant between zero and one.
Consider a finite impulse response (FIR) low pass filter of length N = 201. The following is the Tukey window with α = 0.5.
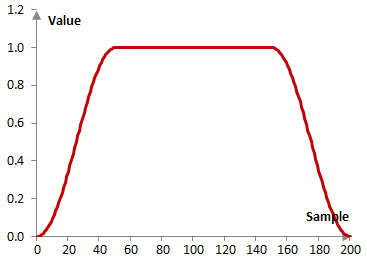
Given a sampling frequency of 2000 Hz and a filter cutoff frequency of 40 Hz, the impulse response of the filter with a rectangular window (with no window) and with the Tukey window above is as follows.
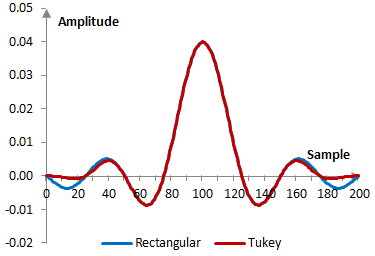
The magnitude response of the same filter is shown on the graph below.
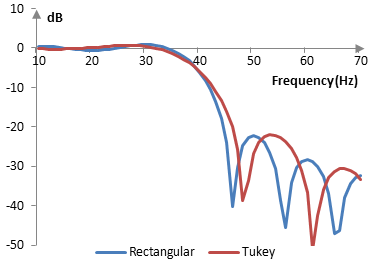
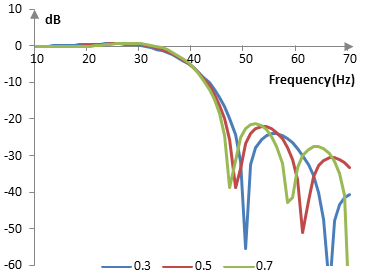
A larger α implies a Tukey window with a "flatter" top, smaller transition band, and worse stop-band attenuation. As α approaches 1, the Tukey window itself approaches a rectangular window. A smaller α creates a Tukey window with a steeper top, larger transition band, and better stop-band attenuation. As α approaches 0, we have
$$a(k)=0.5 (1+\cos(\frac{2\pi|k-\frac{N-1}{2}|}{N-1}))=0.5 (1+\cos(\frac{2 \pi k}{N-1}-\pi))=0.5 (1+\cos(\frac{2 \pi k}{N-1}))$$
аnd the Tukey window approaches the Hann window.
The following is the Tukey window with three different values for α (0.3, 0.5, and 0.7).
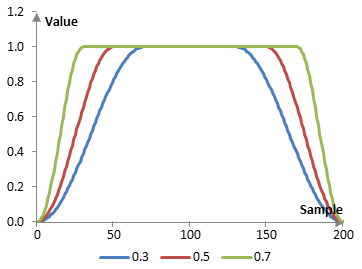
The magnitude response of these same windows given the sampling frequency of 2000 Hz, cutoff frequency of 40 Hz, and a filter of length N = 201 is as follows.
Measures for the Tukey window
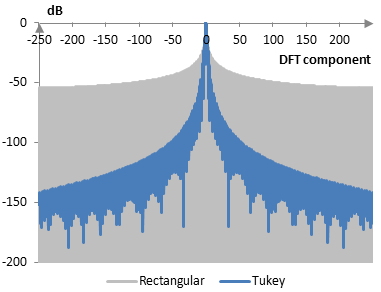
The following is a comparison of the discrete Fourier transform of the Tukey window (α = 0.5) and the rectangular window.
The Tukey window measures are as follows.
| α | 0.3 | 0.5 | 0.7 |
| Coherent gain | 0.65 | 0.75 | 0.85 |
| Equivalent noise bandwidth | 1.33 | 1.22 | 1.13 |
| Processing gain | -1.25 dB | -0.88 dB | -0.52 dB |
| Scalloping loss | -1.81 dB | -2.23 dB | -2.79 dB |
| Worst case processing loss | -3.06 dB | -3.11 dB | -3.31 dB |
| Highest sidelobe level | -18.2 dB | -15.1 dB | -13.8 dB |
| Sidelobe falloff | -16.3 dB / octave, -54.3 dB / decade | -15.8 dB / octave, -52.6 dB / decade | -15.3 dB / octave, -50.9 dB / decade |
| Main lobe is -3 dB | 1.28 bins | 1.16 bins | 1.04 bins |
| Main lobe is -6 dB | 1.76 bins | 1.58 bins | 1.42 bins |
| Overlap correlation at 50% overlap | 0.272 | 0.362 | 0.430 |
| Amplitude flatness at 50% overlap | 0.616 | 0.500 | 0.500 |
| Overlap correlation at 75% overlap | 0.710 | 0.727 | 0.738 |
| Amplitude flatness at 75% overlap | 0.978 | 1.000 | 0.776 |
See also:
Window
Comments
This equation is the opposite
This equation is the opposite of the Wikipedia page.
In this page, alpha is the proportion that is rectangular.
In that page, alpha is the proportion that is trigonometric.
I don't see a "proper definition," so nothing is wrong,
but it might be worth a comment to avoid confusing beginners.
You are correct. In this
You are correct. In this definition, a larger alpha makes the window closer to a rectangular window. A smaller alpha makes it closer to a Hann window. In the Wikipedia definition, it is the opposite. Thanks.
Add new comment