The coefficients of the Poisson window, also called the exponential window, are given by the following formula
$$a(k)=e^{-\alpha \frac{|k-M|}{M}}$$
where N is the length of the filter, M = (N – 1) / 2, k = 0, 1, …, N – 1, and, typically, 0 ≤ α < 1. α is often set to 2 D / 8.69, were D is the desired decay of the window in decibels over half of the window length.
The multiplication of the Poisson window with the Hann window produces the hybrid Hann-Poisson window.
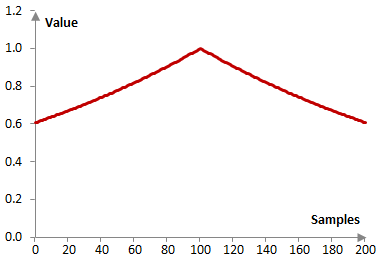
Consider a finite impulse response (FIR) low pass filter of length N = 201. The following is the Poisson window with α = 0.5.
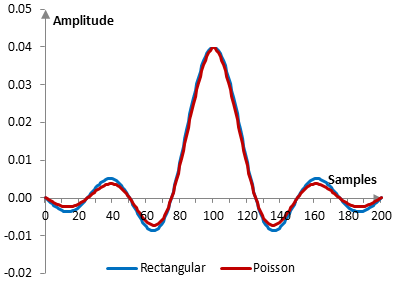
Given a sampling frequency of 2000 Hz and a filter cutoff frequency of 40 Hz, the impulse response of the filter with a rectangular window (with no window) and with the Poisson window is as follows.
The magnitude response of the same filter is shown on the graph below.
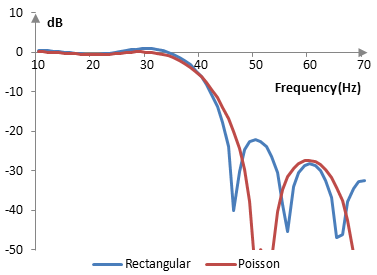
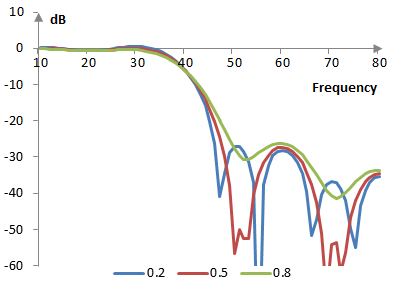
As the parameter α becomes larger, the transition band of the filter with the Poisson window becomes wider and the Gibbs phenomenon ripples in the pass band become smaller. At α = 0, the Poisson window becomes the rectangular window.
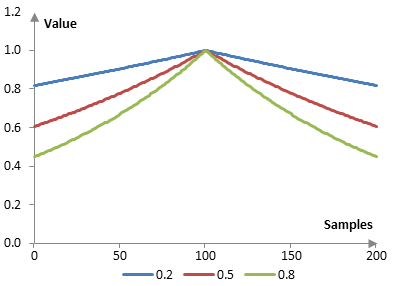
The following is the Poisson window with N = 201 and at three different values of α (0.2, 0.5, and 0.8).
The magnitude response of a filter at these values of α, given a sampling frequency of 2000 Hz and a cutoff frequency of 40 Hz, is shown below.
Measures for the Poisson window
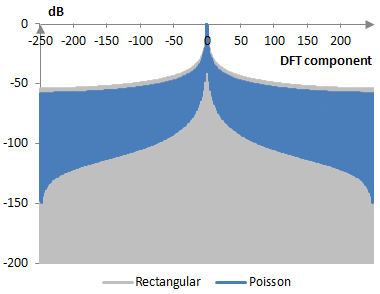
The following is a comparison of the discrete Fourier transform of the Poisson window (α = 0.4) and the rectangular window.
The Poisson window measures are as follows.
| α | 0.2 | 0.5 | 0.8 |
| Coherent gain | 0.91 | 0.79 | 0.69 |
| Equivalent noise bandwidth | 1.00 | 1.02 | 1.05 |
| Processing gain | -0.01 dB | -0.09 dB | -0.22 dB |
| Scalloping loss | -3.69 dB | -3.36 dB | -3.05 dB |
| Worst case processing loss | -3.70 dB | -3.45 dB | -3.27 dB |
| Highest sidelobe level | -14.7 dB | -17.5 dB | -19.9 dB |
| Sidelobe falloff | -6.1 dB / octave, -20.3 dB / decade | -6.3 dB / octave, -20.8 dB / decade | -6.4 dB / octave, -21.4 dB / decade |
| Main lobe is -3 dB | 0.90 bins | 0.94 bins | 1.00 bins |
| Main lobe is -6 dB | 1.24 bins | 1.30 bins | 1.36 bins |
| Overlap correlation at 50% overlap | 0.497 | 0.480 | 0.450 |
| Amplitude flatness at 50% overlap | 0.995 | 0.970 | 0.925 |
| Overlap correlation at 75% overlap | 0.773 | 0.794 | 0.799 |
| Amplitude flatness at 75% overlap | 0.999 | 0.992 | 0.980 |
See also:
Window
Add new comment