The sine window coefficients are given by the following formula
$$a(k)=\sin(\frac{\pi \, k}{N-1})$$
where N is the length of the filter and k = 0, 1, …, N – 1.
The sine window is a power of cosine window. The convolution of the sine window with itself produces the Bohman window.
Consider a finite impulse response (FIR) low pass filter of length N = 201. The following is the sine window.
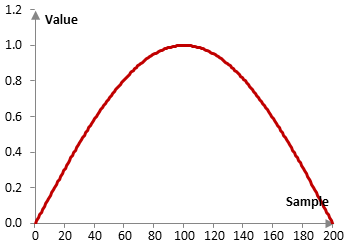
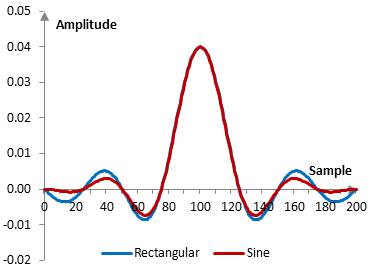
Given a sampling frequency of 2000 Hz and a filter cutoff frequency of 40 Hz, the impulse response of the filter with a rectangular window (with no window) and with the sine window is as follows.
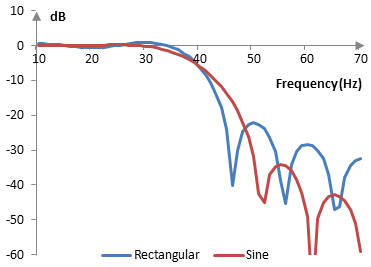
The magnitude response of the same filter is shown on the graph below.
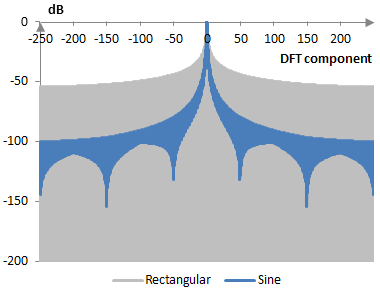
Measures for the sine window
The following graph compares the discrete Fourier transform of the sine window with that of the rectangular window.
The sine window measures are as follows.
| Coherent gain | 0.64 |
| Equivalent noise bandwidth | 1.24 |
| Processing gain | -0.92 dB |
| Scalloping loss | -2.09 dB |
| Worst case processing loss | -3.01 dB |
| Highest sidelobe level | -23.0 dB |
| Sidelobe falloff | -11.2 dB / octave, -37.1 dB / decade |
| Main lobe is -3 dB | 1.18 bins |
| Main lobe is -6 dB | 1.64 bins |
| Overlap correlation at 50% overlap | 0.317 |
| Amplitude flatness at 50% overlap | 0.707 |
| Overlap correlation at 75% overlap | 0.755 |
| Amplitude flatness at 75% overlap | 0.924 |
See also:
Window
Add new comment