Един фейзър е един звукоф ефект, подобен на едно кратко забавяне или хор, но който също наподобява едно уа-уа. Този ефект се получава, като се комбинира изходния сигнал от една поредица от всичкопропускащи филтри с оригиналния сигнал. Филтрите променят фазите на честотите в сигнала и по този начин намаляват амплитудите на определени честоти. Филтрите също променят честотите, амплитудата на които е намалена и тази промяна е подобна на уа-уа.
Пример на един фейзър със звуково парче
Виж Orinj Фейзър за да чуеш едно звуково парче преди и след един фейзър.
Конструкция на фейзъра
Един фейзър комбинира входния сигнал с изхода на една поредица от всичкопропускащи филтри със затихвания, които се колебаят. Примери на такива всичкопропускащи филтри са по-долу.
- Всичкопропускащите филтри променят фазите на честотите в сигнала. Заради това, когато резултатът е комбиниран с оригиналния сигнал, амплитудите на някои честоти намаляват, а амплитудите на други честоти се запазват. Амплитудният спектър на целия ефект е подобен на този на едно кратко забавяне или гребенов филтър. Този спектър има върхове, където амплитудите на честотите са запазени и бразди, където амплитудите на честотите са значително намалени.
- Параметрите на всичкопропускащите филтри се променят с времето. Това кара браздите на амплитудния спектър да се местят наляво и надясно. Това движение произвежда звук като едно уа-уа.
Фейзъра има две характеристики – едно оцветяване на звука подобно на едно кратко забавяне и едно колебание като в едно уа-уа. Коя от тези две характеристики е по-забележима зависи от броя, вида и местоположението (в честотния диапазон) на филтрите и скоростта и амплитуда на колебанието на параметрите на филтрите. Уа-уа-то например може да не е забележимо, ако колебанията са много бавни.
Параметри на фейзъра
- Скорост, колебание или LFO: Един фейзър поне ще позволи на потребителя да контролира честотата на колебанието във филтрите.
- Амплитуда или сух и мокър микс: Доста от фейзърите позволяват да се контролира относителната амплитуда на оригиналния сигнал спрямо амплитудата на изхода от поредицата от филтри.
- Разпределение или фактор Q: По-гъвкавите фейзъри може да позволят да се контролира разпределението на браздите в амплитудния спектър (виж Еквилайзер за описание на термина фактор Q).
- Дълбочина или помитане: Някои фейзъри може да позволят да се контролира амплитудата на колебанието.
- Център, помитане или ширина: Някои фейзъри може да позволят да се контролира къде е центъра на браздите в амплитудния спектър.
- Стерео, обратна връзка или ротация: Някои фейзъри може да позволят да има някаква връзка между сигналите в каналите.
Един фейзър може също да използва един единствен контрол за да променя няколко от тези параметри заедно, в зависимост от предпочитанията на този, който го е създал.
Един примерен всичкопропускащ филтър в непрекъснато време за един фейзър
Следното е трансферната функция на един всичко пропускащ филтър в непрекъснато време, който може да се използва в един фейзър.
$$H(s) = \frac{s-\omega_0}{s+\omega_0}$$
Това е един всичкопропускащ филтър от първи разряд.
Това наистина е всичкопропускащ филтър, защото амплитудният му спектър е
$$H(j \, \omega) = |\frac{j \, \omega-\omega_0}{j \, \omega+\omega_0}|=|\frac{-(\omega_0-j \, \omega)^2}{\omega^2+\omega_0^2}|$$ $$=|\frac{\omega^2+2\,j \, \omega_0 \, \omega-\omega_0^2}{\omega^2+\omega_0^2}|=|\frac{\sqrt{(\omega^2-\omega_0^2)^2+(2 \, \omega_0 \, \omega)^2}}{\omega^2+\omega_0^2}|=1$$
Фазовият спектър на този филтър е
$$\Theta(\omega)=\mathrm{atan2}(\frac{Im(H)}{Re(H)})=\mathrm{atan2}(\frac{2\,\omega_0 \, \omega}{\omega^2-\omega_0^2})$$
Фазовият спектър е π при ω = 0, намалява до π / 2 при ω = ω0 и намалява след това, когато ω се увеличава. Следното е една графика на фазовия спектър между 0 Hz и 250 Hz при ω0 = 100 Hz (непрекъсната линия) и ω0= 200 Hz (прекъснатата линия).
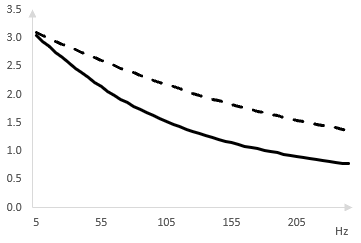
Промяната във фазата заради всичкопропускащия филтър е важна. Добавянето на изходния сигнал от всичкопропускащия филтър към оригиналния сигнал е събиране на два сигнала с различна фаза. Амплитудата на честотите в резултата се променя в зависимост от промяната във фазата. Колко по-ниска е честотата, толкова по-близо промяната във фазата е до π, толкова по-близо е изхода от всичкопропускащия филтър към една вълна с обърната фаза и толкова по-ниска е амплитудата на резултата. Добавянето на изходния сигнал от всичкопропускащия филтър към оригиналния сигнал създава един високочестотен филтър. Една графика на това е показана по-долу.
Високочестотният филтър е резултатът от добавянето на оригиналния сигнал към изходния сигнал на един единствен всичкопропускащ филтър. Една поредица от няколко всичкопропускащи филтри създава един по-сложен амплитуден спектър. Амплитудния спектър е такъв, че някои ленти от честоти се запазват, а други ленти от честоти са с намалена амплитуда, което създава бразди в амплитудния спектър. Браздите се местят, когато параметрите на всичкопропускащите филти се променят и така работи фейзъра. Това е показано по-долу.
Това е един примерен всичкопропускащ филтър и други такива филтри са възможни.
Един примерен всичкопропускащ филтър в дискретизирано време
Използвай билинейното преобразуване за да създадеш един дискретизиран цифров всичкопропускащ филтър от филтъра в непрекъснато време по-горе.
$$s=\frac{2(z-1)}{z+1}$$ $$H(z)=\frac{\frac{2(z-1)}{z+1}-\omega_0}{\frac{2(z-1)}{z+1}+\omega_0}=\frac{(2-\omega_0)z-2-\omega_0}{(2+\omega_0)z-2+\omega_0}$$
Определи d = (2 - ω0) / (2 + ω0). Забележи обаче, че билинейното преобразуване изкривява честотния спектър и се справи с това като заместиш ω0 с 2 tan(ω0 / 2) (виж Билинейно преобразуване).
$$H(z)=\frac{d-z^{-1}}{1- d\, z^{-1}}, \, \, d=\frac{1-\tan(\frac{\omega_0}{2})}{1+\tan(\frac{\omega_0}{2})}$$
Този филтър изчислява изходния сигнал y при проба k от входния сигнал x по следния начин.
$$y(k)=d \, x(k)-x(k-1)+ d \, y(k-1)$$
d е една константа, която умножава текущата проба на входния сигнал x и можем да я наречем затихването на филтъра. (Това по същество е специален случай на всичкопропускащия филтър на Шрьодер, описан в темата Всичкопропускащ филтър).
Един примерен фейзър
Използваме дискретизирания всичкопропускащ филтър по-горе за да създадем един фейзър. Първо преглеждаме изходния сигнал на един фейзър само с един всичкопропускащ филтър и след това добавяме още всичкопропускащи филтри.
Следното е амплитудния спектър на един фейзър само с един всичкопропускащ филтър от първи разряд. Както очакваме, събирането на оригиналния сигнал с изходния сигнал от един единствен всичкопропускащ филтър просто създава един високочестотен филтър. В този пример, използваме ω0 = 50 Hz (пробната честота е 500 Hz).
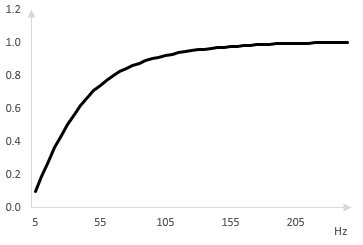
Да предположим, че вместо един филтър, използваме два всичкопропускащи филтри в поредица. Изходният сигнал от първия всичкопропускащ филтър става входния сигнал във втория всичкопропускаш филтър. Изходният сигнал от втория всичкопропускащ филтър се събира с оригиналния сигнал за да създаде изходния сигнал от фейзъра. Разделяме двата всичкопропускащи филтри съответно с ω0 = 50 Hz и 100 Hz. Амплитудният спектър на фейзъра е следния.
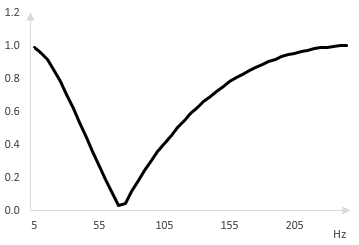
Добавяме още два всичкопропускащи филтъра. Следното е амплитудния спектър на един фейзър с четири всичкоропускащи филтри, сложени при ω0 = 50, 100, 150 и 200 Hz.
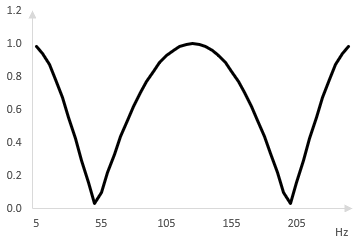
Колебание във фейзъра
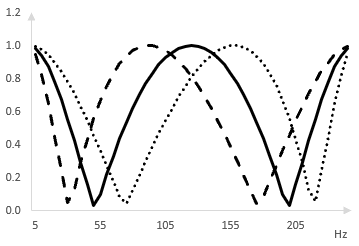
Когато централните честоти на всичкопропускащите филтри се колебаят (наляво и надясно), браздите в амплитудния спектър се местят (съответно наляво и надясно). Следното е същия амплитуден спектър (непрекъснат), показан когато централните честоти на всичкопропускащите филтри са преместени наляво с Hz (прекъснат) и надясно с 25 Hz (с точки).
Добави нов коментар