The Hamming window coefficients are given by the following formula
$$w(k)=0.54-0.46 \, \cos(\frac{2\pi\,k}{N-1})$$
where N is the length of the filter and k = 0, 1, …, N – 1.
An example Hamming window
Consider a finite impulse response (FIR) low pass filter of length N = 201. The following is the Hamming window.
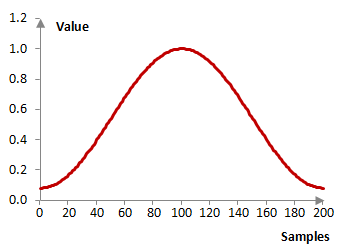
Given a sampling frequency of 2000 Hz and a filter cutoff frequency of 40 Hz, the impulse response of the filter with a rectangular window (with no window) and with the Hamming window is as follows.
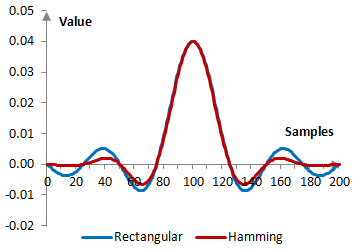
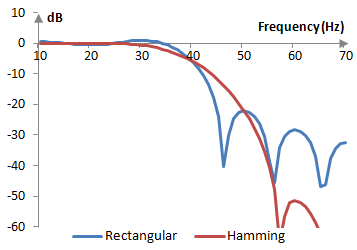
The magnitude response of the same filter is shown on the graph below.
Deriving the Hamming window
The usual purpose of windows is to mitigate the ripples of the Gibbs phenomenon, which are the result of the Fourier series approximation, a series of continuous functions, over the discontinuous desired magnitude response. To decrease these ripples, we will soften the discontinuity. Rather than creating a filter with the inverse Fourier transform of the ideal desired magnitude response (in blue below), we will use a revised magnitude response (in red below).
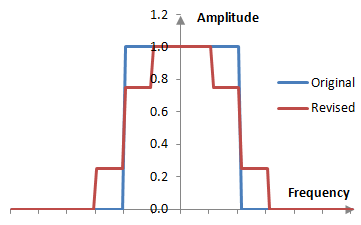
We can recognize that the revised magnitude response is the sum of the scaled original magnitude response H with two scaled and shifted versions of itself.
$$\alpha \, H(f)+\beta \, H(f-f_0)+\beta \, H(f+f_0)$$
where α is the scaling factor for the original magnitude response, β is the scaling factor for the shifted magnitude responses, and f0 and –f0 are the two shifts. In the example above, α = 0.5, β = 0.25, and f0 = ¼ fc, where fc is the cutoff frequency.
We can also note that the windowed filter is the product of the filter and the window. If the windowed filter was to be created with the inverse Fourier transform from a desired magnitude response, then the desired magnitude response must be a convolution of the Fourier transform of the filter and the Fourier transform of the window (more precisely, the Fourier transform of a product is a period / circular convolution). We rewrite the revised magnitude response above as a convolution as follows.
$$H(f) * (\alpha \, \delta(f)+\beta \, \delta(f-f_0)+\beta \, \delta(f+f_0))$$
where δ is the Dirac delta function (we use the Dirac delta function, as it allows us to both write result in terms of a convolution, as well as to recognize the transform of the cosine function in the last two terms). The inverse Fourier transform of this desired magnitude response is the filter before the window, multiplied by the window
$$w(k)=\alpha+2\,\beta \frac{\cos(f_0 \, k)}{\pi}$$
This is the Hamming window family, which includes the Hamming window itself and the Hann window. This generalized Haming window is more often written as follows.
$$w(k)=\alpha-\beta \, \cos(\frac{2\pi\,k}{N-1})$$
The Hamming family windows are also "generalized cosine windows", which are windows of the form
$$w(k)=\sum_{m=0}^{M} a_m \, \cos(\frac{2\pi\,m\,k}{N-1})$$
M denotes the order of the window. These include the Blackman window, the Nuttall window, the Blackman-Nuttall window, the Blackman-Harris window, the Rife-Vincent windows, and certain flat top windows. The rectangular window can also be considered a generalized cosine window (of order 0).
Measures for the Hamming window
The discrete Fourier transform of the Hamming window over the discrete Fourier transform of the rectangular window is shown on the graph below.
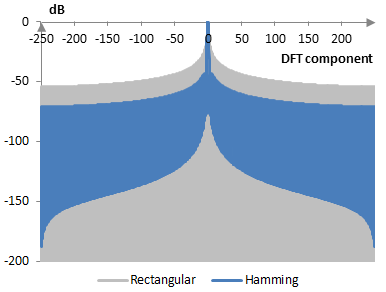
The measures of the Hamming window are as follows.
| Coherent gain | 0.54 |
| Equivalent noise bandwidth | 1.36 |
| Processing gain | -1.35 dB |
| Scalloping loss | -1.75 dB |
| Worst case processing loss | -3.10 dB |
| Highest sidelobe level | -44.4 dB |
| Sidelobe falloff | -7.9 dB / octave, -26.1 dB / decade |
| Main lobe is -3 dB | 1.30 bins |
| Main lobe is -6 dB | 1.82 bins |
| Overlap correlation at 50% overlap | 0.233 |
| Amplitude flatness at 50% overlap | 1.000 |
| Overlap correlation at 75% overlap | 0.706 |
| Amplitude flatness at 75% overlap | 1.000 |
See also:
Window
Add new comment