The Hann-Poisson window coefficients are given by the following formula
$$a(k)=0.5 * (1-\cos(\frac{\pi\,k}{M}))\,e^{-\alpha\frac{|k-M|}{M}}$$
where N is the length of the filter, M = (N – 1) / 2, k = 0, 1, …, N – 1, and usually 0 ≤ α < 1.
The Hann-Poisson window is the product of the Hann window and the Poisson window.
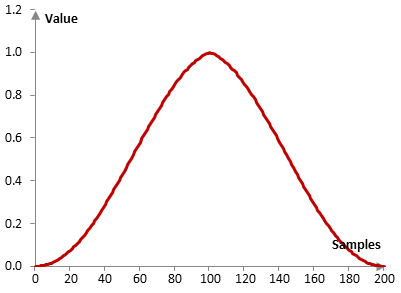
An example Hann-Poisson window
Consider a finite impulse response (FIR) low pass filter of length N = 201. The following is the Hann-Poisson window with α = 0.3.
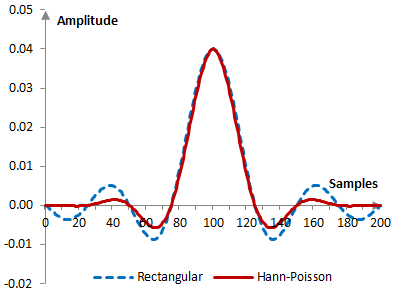
Given a sampling frequency of 2000 Hz and a filter cutoff frequency of 40 Hz, the impulse response of the filter with a rectangular window (with no window) and with the Hann-Poisson window is as follows.
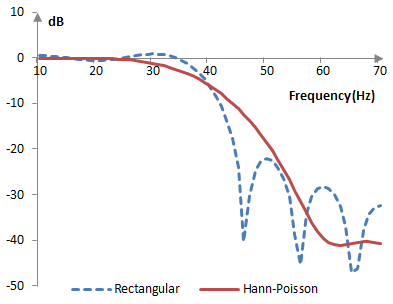
The magnitude response of the same filter is shown on the graph below.
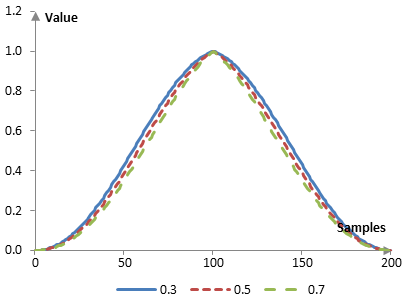
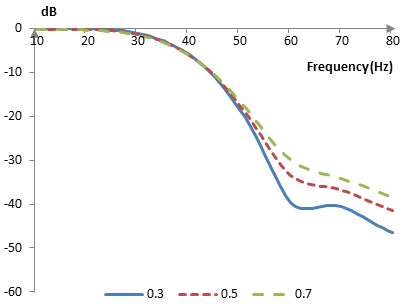
As the parameter α becomes larger, the transition band of the Hann-Poisson window increases and its Gibbs phenomenon ripples become smaller.
The following is the Hann-Poisson window with N = 201 and at three different values of α (0.3, 0.5, and 0.7).
The magnitude response of a filter at these values of α, given a sampling frequency of 2000 Hz and a cutoff frequency of 40 Hz, is shown below.
Measures for the Hann-Poisson window
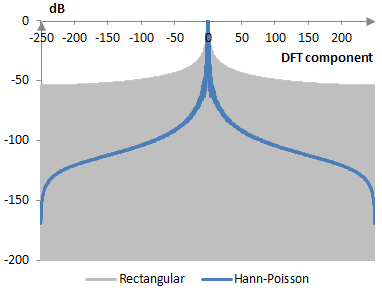
The following is a comparison of the discrete Fourier transform of the Hann-Poisson window and the rectangular window.
The Hann-Poisson window measures are as follows.
| α | 0.3 | 0.5 | 0.7 |
| Coherent gain | 0.46 | 0.43 | 0.41 |
| Equivalent noise bandwidth | 1.57 | 1.61 | 1.66 |
| Processing gain | -1.95 dB | -2.07 dB | -2.20 dB |
| Scalloping loss | -1.32 dB | -1.25 dB | -1.19 dB |
| Worst case processing loss | -3.27 dB | -3.33 dB | -3.40 dB |
| Highest sidelobe level | -37.6 dB | -35.2 dB | -33.0 dB |
| Sidelobe falloff | -17.4 dB / octave, -57.7 dB / decade | -16.8 dB / octave, -55.9 dB / decade | -16.4 dB / octave, -54.6 dB / decade |
| Main lobe is -3 dB | 1.50 bins | 1.54 bins | 1.58 bins |
| Main lobe is -6 dB | 2.08 bins | 2.14 bins | 2.20 bins |
| Overlap correlation at 50% overlap | 0.140 | 0.124 | 0.110 |
| Amplitude flatness at 50% overlap | 0.861 | 0.779 | 0.705 |
| Overlap correlation at 75% overlap | 0.631 | 0.612 | 0.591 |
| Amplitude flatness at 75% overlap | 0.977 | 0.960 | 0.942 |
See also:
Window
Comments
Older comments
admin: First posted on 2014 04 20
mic, 2014 04 20: I've just fixed this topic. The previous version of the topic was wrong - it was missing a minus before the alpha parameter. the window still worked, but it wasn't the Hann-Poisson window.
Add new comment