Коефициентите на плоския прозорец се дават от формулата
$$a(k)= 0.21557895-0.41663158 \, \cos(\frac{2 \pi k}{N-1})+0.277263158 \, \cos(\frac{4 \pi k}{N-1})$$ $$- 0.083578947 \, \cos(\frac{6 \pi k}{N-1}) + 0.006947368 \, \cos(\frac{8 \pi k}{N-1})$$
където N е дължината на филтъра и k = 0, 1, …, N – 1.
Един примерен плосък прозорец
Вземи един нискочестотен филтър с ограничен импулсен спектър (FIR) и с дължина N = 201. Следното е плоският прозорец.
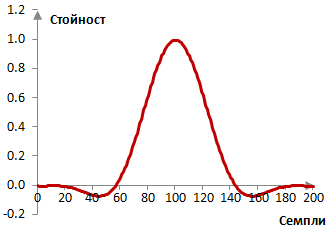
Ако пробната честота е 2000 Hz и преходната честота на филтъра е 40 Hz, тогава импулсният спектър на филтъра с правоъгълен прозорец (без прозорец) и с плоския прозорец е както следва.
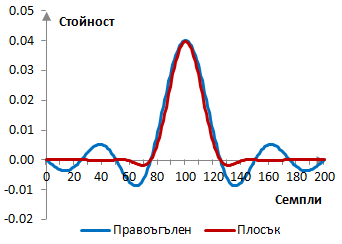
Амплитудният спектър на съшия филтър е показан в графиката по-долу.
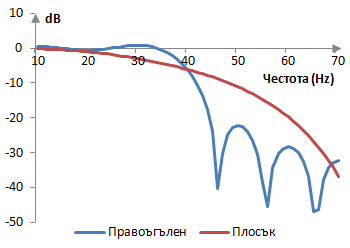
Измерения за плоския прозорец
Следната графика показва дискретизираното преобразуване на Фурие на плоския прозорец върху преобразуването на правоъгълния прозорец.
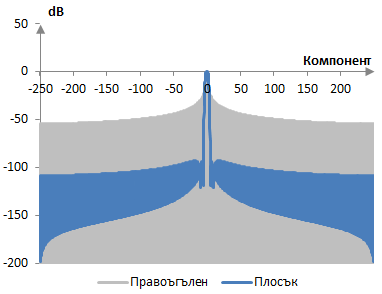
Следното са подбрани измерения за плоския прозорец.
| Кохерентна амплитуда | 0.22 |
| Еквивалентна лента на шума | 3.78 |
| Загуба при преработката | -5.77 dB |
| Загуба на лоба | -0.01 dB |
| Загуба при преработката в най-лошия случай | -5.78 dB |
| Ниво на най-високия страничен лоб | -93.6 dB |
| Спадане на страничните лобове | -12.1 dB / октава, -40.1 dB / декада |
| Главният лоб е -3 dB | 3.72 компонента |
| Главният лоб е -6 dB | 4.00 компонента |
| Корелация при застъпването при застъпване от 50% | -0.015 |
| Амплитудна гладкост при застъпване от 50% | -0.110 |
| Корелация при застъпването при застъпване от 75% | 0.044 |
| Амплитудна гладкост при застъпване от 75% | 0.938 |
Виж също:
Прозорец
Добави нов коментар