Когато използваме преобразуването на Фурие за да анализираме честотното съдържание на един сигнал, към сигнала често първо се прилагат прозорци за да се направи преобразуването на Фурие по прецизно. По същите причини, отсечките на сигнала, към които се прилага преобразуването на Фурие, обикновено са избрани така, че да се застъпват. В зависимост от това, как е избрано застъпването, застъпващите се прозорци променят амплитудата на сигнала. Тази промяна е различна при различните проби на сигнала.
Амплитудната гладкост на един прозорец е отношението на минималната амплитуда към максималната амплитуда, която е приложена към проби на сигнала при използването на прозорци.
Следната графика например показва шест прозорци на Хан с дължина 50, които се застъпват с 40% (с 20 проби). Цялата амплитуда, която конфигурацията на тези прозорци ще даде на всяка от пробите на сигнала варира между 0.69 в средата между прозорците и 1 при върха на всеки прозорец (пунктираната линия по-долу; тази цяла амплитуда е просто сумата на стойностите на прозорците върху оста на времето).
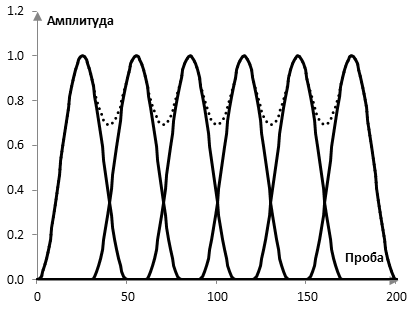
Така, амплитудната гладкост на прозореца на Хан при 40% застъпване е 0.69. Това число ще се увеличи, когато застъпването се увеличи.
Оптимално застъпване
С прозореца на Хан, когато застъпването е 50%, амплитудната гладкост е 1. С други думи, цялата амплитуда, която е приложена от прозорците към всяка от пробите е една и съща (тя е 1). Между другото, с това застъпване, разликата между амплитудната гладкост и корелацията при застъпването на прозореца на Хан е най-голяма. Застъпването от 50% понякога се нарича "оптимално застъпване" на прозореца на Хан, в смисъла, че дава максималната амплитудна гладкост за минималната корелация на застъпването. Максималната амплитудна гладкост означава, че амплитудата е една и съща (за прозореца на Хан, почти една и съща при повечето от другите прозорци) и следователно нито една от пробите не е по-маловажна в спектралния анализ – не се губят данни. Минималната корелация на застъпването означава, че няма ненужно застъпване и изчислителна интензивност при спектралния анализ. "Оптималното застъпване" тогава е застъпването, което дава сравнително малка загуба на данните за сравнително малко изчисления. Едно застъпване, при което амплитудната гладкост става 1, обикновено не съществува при другите прозорци. Оптималното застъпване обаче може да се изчисли по същия начин.
Мощностна гладкост
Мощностната гладкост на прозореца се определя по същия начин, но вместо да се събират стойностите на застъпените прозорци, се събират квадратите на тези стойности. Мощностната гладкост е по-подходяща за сигнали, които не наподобяват синусоиди толкова, колкото наподобяват шум.
Амплитудна гладкост за често срещани прозорци
Следното е амплитудната гладкост на често срещани прозорци (при 50% застъпване, при 75% застъпване, с определенията на прозорците в този сайт).
| Бартлет и Хан | 1.000, 1.000 |
| Блекмън Точен Блекмън Обобщен Блекмън α = 0.05 α = 0.20 α = 0.35 |
0.680, 1.000 0.695, 1.000 0.900, 1.000 |
| Блекмън и Харис | 0.435, 1.000 |
| Блекмън и Нътол | 0.454, 1.000 |
| Боумън | 0.637, 0.982 |
| Долф и Чебишев ω0 = 0.1 ω0 = 0.2 ω0 = 0.3 |
0.272, 0.914 0.154, 0.579 0.127, 0.377 |
| Плосък | -0.110, 0.938 |
| Гаус σ = 0.3 σ = 0.5 σ = 0.7 Приблизителен ограничен на Гаус σ = 0.3 σ = 0.5 σ = 0.7 Обобщен нормален α = 2 α = 4 α = 6 |
0.497, 0.998 0.936, 0.973 0.878, 0.969 0.498, 0.998 0.936, 0.973 |
| Хеминг | 1.000, 1.000 |
| Хан | 1.000, 1.000 |
| Хан и Поасон α = 0.3 α = 0.5 α = 0.7 |
0.861, 0.977 0.779, 0.960 0.705, 0.942 |
| Кайзер α = 0.5 α = 1.0 α = 5.0 |
0.895, 0.974 0.829, 0.958 0.691, 0.991 |
| Кайзер и Бесел | 0.608, 1.000 |
| Ланцош | 0.785, 0.947 |
| Нътол | 0.423, 1.000 |
| Парзън | 0.869, 0.966 |
| Клин на Планк ε = 0.2 ε = 0.4 ε = 0.5 |
0.500, 0.860 0.672, 0.923 1.000, 1.000 |
| Поасон α = 0.2 α = 0.5 α = 0.8 |
0.995, 0.999 0.970, 0.992 0.925, 0.980 |
| Степен на косинуса α = 1.0 α = 2.0 α = 3.0 |
0.707, 0.924 1.000, 1.000 0.707, 0.990 |
| Правоъгълен | 1.000, 1.000 |
| Синусоиден | 0.707, 0.924 |
| Триъгълен | 1.000, 1.000 |
| Тъки α = 0.3 α = 0.5 α = 0.7 |
0.616, 0.978 0.500, 1.000 0.500, 0.776 |
| Ултрасферичен (x0 = 1) μ = 2 μ = 3 μ = 4 |
0.684, 0.914 0.859, 0.982 0.908, 0.992 |
| Уелч | 0.670, 0.910 |
Добави нов коментар