Загубата на лоба на един прозорец a(k) с дължина N е
$$SL=\frac{|\sum_{k=0}^{N-1}a(k) e^{-\frac{j \pi k}{N}}|}{\sum_{k=0}^{N-1}a(k)}=\frac{\sqrt{(\sum_{k=0}^{N-1} a(k) \cos(\frac{\pi k}{N}))^2+(\sum_{k=0}^{N-1} a(k) \sin(\frac{\pi k}{N}))^2}}{\sum_{k=0}^{N-1} a(k)}$$
Загубата на лоба е кохерентната амплитуда на една честота, която по средата между два компонента на дискретизираното преобразуване на Фурие, разделена на кохерентната амплитуда на прозореца, както е обяснено по-долу.
Обосновка на загубата на лоба
Следното е графика на максималната стойност на дискретизираното преобразуване на Фурие от 40 точки върху прости синусоиди с различни честоти между 20 Hz и 80 Hz, като пробната честота е 400 Hz.
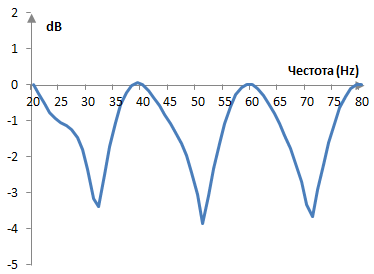
Графиката наподобява един фестон (от англ., "scallop"; украсяващите лупинги на пердетата или покривките). Най-голямата "загуба", местата където преобразуването на Фурие е най-непрецизно, е (приблизително) в средата между компонентите на преобразуването. При пробната честота 400 Hz, едно преобразуване от 40 точки ще има компоненти 0 Hz, 20, Hz, 40, Hz, …, 380 Hz. Най-голямата загуба е при 30 Hz, 50 Hz и така нататък. Така, загубата на лоба е най-голямата загуба, която се дължи на честотата.
Загубата на лоба и прозорците
Вземи следната графика.
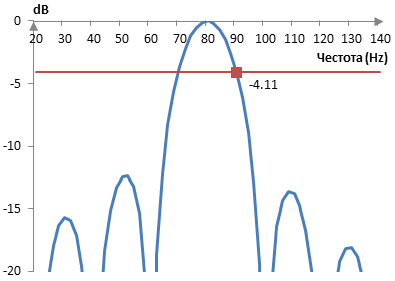
Това е дискретизираното преобразуване на Фурие от 20 компонента на синусоидата с честота 80 Hz, дискретизирана с пробната честота 400 Hz. Вместо да вземе преобразуването на вълната само при 20-те компонента обаче (0 Hz, 20 Hz, 40 Hz, …, 380 Hz), графиката показва преобразуването и при честоти между компонентите. Ако преобразуването беше изчислено само при честотите на компонентите, тогава графиката щеше да покаже само 0 dB при 80 Hz и на практика доста големи отрицателни числа при всички други компоненти. Между компонентите обаче, има спектрално разсейване. По средата между компонентите, получаваме -4.11 dB. Това е загубата на лоба без прозорец (с правоъгълния прозорец).
Да предположим, че използваме прозореца на Хан от 20 точки върху синусоидата преди да изчислим дискретизираното преобразуване на Фурие. Резултатът е показан в следната графика. Преобразуването след прозореца на Хан е показано с една непрекъсната линия. Преобразуването без прозореца е с една пунктирана линия.
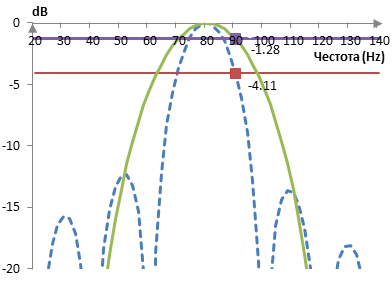
Преобразуването след прозореца на Хан в тази графика е настроено с кохерентната амплитуда на прозореца. Загубата на лоба с прозореца на Хан е -1.28 dB. Така, загубата на лоба е измерение за формата на главния лоб на преобразуването на Фурие на прозореца.
Този пример, разбира се, изчислява загубата на лоба по-средата между два случайно избрани компоненти и при един доста къс прозорец. С формулата по-горе и при по-дълги прозорци, загубата на лоба на прозореца на Хан ще бъде приблизително -1.42 dB (обикновено записана без минуса, тъй като е "загуба").
Загуба на лоба при често срещани прозорци
Следната таблица показва загубата на лоба (в децибели) за някои от често срещаните прозорци (с определенията на тези прозорци, дадени в този сайт).
| Бартлет и Хан | -1.51 |
| Блекмън Точен Блекмън Обобщен Блекмън α = 0.05 α = 0.20 α = 0.35 |
-1.09 -1.15 -1.33 |
| Блекмън и Харис | -0.82 |
| Блекмън и Нътол | -0.85 |
| Боумън | -1.02 |
| Долф и Чебишев ω0 = 0.1 ω0 = 0.2 ω0 = 0.3 |
-1.44 -1.28 -1.23 |
| Плосък | -0.01 |
| Гаус σ = 0.3 σ = 0.5 σ = 0.7 Приблизителен ограничен на Гаус σ = 0.3 σ = 0.5 σ = 0.7 Обобщен нормален α = 2 α = 4 α = 6 |
-0.95 -2.12 -2.84 -0.95 -2.12 |
| Хеминг | -1.75 |
| Хан | -1.42 |
| Хан и Поасон α = 0.3 α = 0.5 α = 0.7 |
-1.32 -1.25 -1.19 |
| Кайзер α = 0.5 α = 1.0 α = 5.0 |
-3.31 -2.42 -1.05 |
| Кайзер и Бесел | -1.02 |
| Ланцош | -1.88 |
| Нътол | -0.81 |
| Парзън | -2.57 |
| Клин на Планк ε = 0.2 ε = 0.4 ε = 0.5 |
-2.46 -1.51 -1.20 |
| Поасон α = 0.2 α = 0.5 α = 0.8 |
-3.69 -3.36 -3.05 |
| Степен на косинуса α = 1.0 α = 2.0 α = 3.0 |
-2.09 -1.42 -1.07 |
| Правоъгълен | -3.92 |
| Синусоиден | -2.09 |
| Триъгълен | -1.82 |
| Тъки α = 0.3 α = 0.5 α = 0.7 |
-1.81 -2.23 -2.79 |
| Ултрасферичен (x0 = 1) μ = 2 μ = 3 μ = 4 |
-2.32 -1.66 -1.30 |
| Уелч | -2.23 |
Добави нов коментар