Корелацията при застъпването на един прозорец w(k) се изчислява с формулата
$$OC(r)=\frac{\sum_{k=0}^{rN-1} w(k)\,w(k+(1-r)N)}{\sum_{k=0}^{N-1}(w(k))^2}$$
където N е дължината на прозореца и r е стойността на застъпването, 0 < r ≤ 1.
Когато един сигнал се анализира с преобразуването на Фурие, често вземаме преобразуването на Фурие на застъпващи се отсечки от сигнала. Това има предимства. Можем да покажем, например, че със застъпващи се отсечки преобразуването на Фурие е по прецизно при определянето на вярната честота и фаза на сигнала. Едно друго предимство е, че ако един прозорец се приложи върху сигнала преди преобразуването на Фурие, загубата на информация е по-малка когато има застъпване. Тази загуба на информация се получава, защото краищата на прозореца потискат амплитудата на сигнала.
В следната графика например, преобразуването на Фурие от 50 компонента се прилага четири пъти върху 200 проби на сигнала, с четири отсечки, които не се застъпват и прозорецът на Хан се използва преди преобразуването. Прозорецът на Хан нулира сигнала при пробите 0, 50, 100, 150 и 200 и значително понижава стойностите на сигнала около тези проби.
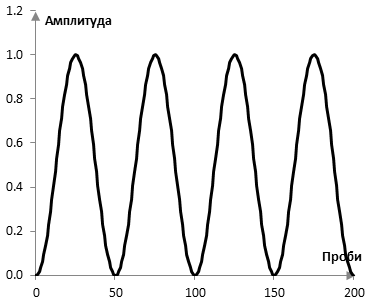
Това може да се избегне, ако отсечките на преобразуването на Фурие се застъпват. С прозореца на Хан, всъщност, едно застъпване от 50% има хубавото свойство, че сумата на тежестите приложени върху всяка от пробите на сигнала е точно 1 (такова застъпване обикновено не съществува при другите прозорци). Проблемът с по-големите застъпвания е, че преобразуването на Фурие, което изисква доста изчисления, трябва да се използва много повече пъти. Въпреки че преобразуването на Фурие от 50 компонента върху 200 проби без застъпване трябва да се изчисли четири пъти, с 50% застъпване, ще бъде изчислено 8 пъти, както в следващата графика.
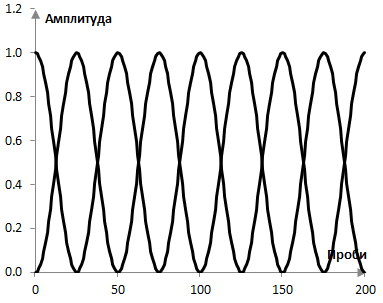
Също така, два съседни преобразувания произвеждат подобни резултати. Колкото по-голямо е застъпването, толкова по-подобни са резултатите. В този смисъл, прекалено много застъпване изисква допълнителни изчисления без допълнителна полза.
Корелацията при застъпване е корелацията на стойностите на два съседни преобразувания. Корелацията при застъпване на прозореца на Хан с r = 0.5 например е 0.165. С по-голямо застъпване, тази корелация е по-голяма. При r = 0.75, корелацията е 0.658. (Виж Амплитудна гладкост за една дискусия на оптималното застъпване).
Корелация при застъпването за често срещани прозорци
Следното е корелацията при застъпването за често срещани прозорци (при 50% застъпване, при 75% застъпване, с определенията на прозорците в този сайт).
| Бартлет и Хан | 0.186, 0.674 |
| Блекмън Точен Блекмън Обобщен Блекмън α = 0.05 α = 0.20 α = 0.35 |
0.089, 0.565 0.099, 0.576 0.143, 0.635 |
| Блекмън и Харис | 0.037, 0.459 |
| Блекмън и Нътол | 0.041, 0.469 |
| Боумън | 0.073, 0.544 |
| Долф и Чебишев ω0 = 0.1 ω0 = 0.2 ω0 = 0.3 |
0.155, 0.440 0.120, 0.261 0.102, 0.201 |
| Плосък | 0.015, 0.044 |
| Гаус σ = 0.3 σ = 0.5 σ = 0.7 Приблизителен ограничен на Гаус σ = 0.3 σ = 0.5 σ = 0.7 Обобщен нормален α = 2 α = 4 α = 6 |
0.060, 0.498 0.311, 0.755 0.431, 0.801 0.059, 0.497 0.311, 0.755 |
| Хеминг | 0.233, 0.706 |
| Хан | 0.165, 0.658 |
| Хан и Поасон α = 0.3 α = 0.5 α = 0.7 |
0.140, 0.631 0.124, 0.612 0.110, 0.591 |
| Кайзер α = 0.5 α = 1.0 α = 5.0 |
0.479, 0.794 0.370, 0.783 0.080, 0.559 |
| Кайзер и Бесел | 0.072, 0.537 |
| Ланцош | 0.272, 0.733 |
| Нътол | 0.035, 0.452 |
| Парзън | 0.393, 0.792 |
| Клин на Планк ε = 0.2 ε = 0.4 ε = 0.5 |
0.392, 0.721 0.202, 0.666 0.115, 0.614 |
| Поасон α = 0.2 α = 0.5 α = 0.8 |
0.497, 0.773 0.480, 0.794 0.450, 0.799 |
| Степен на косинуса α = 1.0 α = 2.0 α = 3.0 |
0.317, 0.755 0.165, 0.568 0.084, 0.565 |
| Правоъгълен | 0.500, 0.752 |
| Синусоиден | 0.317, 0.755 |
| Триъгълен | 0.248, 0.718 |
| Тъки α = 0.3 α = 0.5 α = 0.7 |
0.272, 0.710 0.362, 0.727 0.430, 0.738 |
| Ултрасферичен (x0 = 1) μ = 2 μ = 3 μ = 4 |
0.359, 0.772 0.223, 0.702 0.138, 0.632 |
| Уелч | 0.345, 0.765 |
Добави нов коментар