Спадането на страничните лобове на един прозорец е скоростта, с която амплитудата на страничните лобове на дискретизираното преобразуване на Фурие на прозореца намалява.
Начинът, по който спадането на страничните лобове на прозорците в този сайт е изчислено, е прост. Ако предположим, че дискретизираното преобразуване на Фурие на прозореца е настроено така, че върхът на главния лоб на преобразуването е 0 dB, спадането на страничните лобове е изчислено като отношението на върха на последния лоб (в децибели) към броя на октавите или декадите в преобразуването. Така, спадането на страничните лобове се измерва в децибели в една октава или децибели в една декада. Октавите или декадите на дискретизираното преобразуване на Фурие са изчислени с log2(N/2) или log10(N/2), където N е дължината на преобразуването.
Следното например е дискретизираното преобразуване на Фурие от 500 компонента на правоъгълния прозорец.
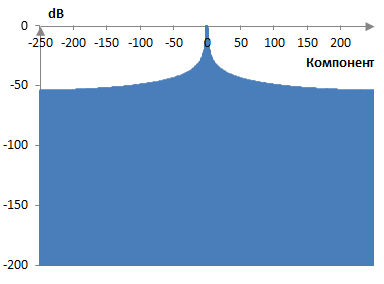
Ако се приближим и изчислим преобразуването също така и в точки между компонентите на преобразуването, ще видим лобовете. Следната графика показва главния лоб и няколко от страничните лобове на преобразуването.
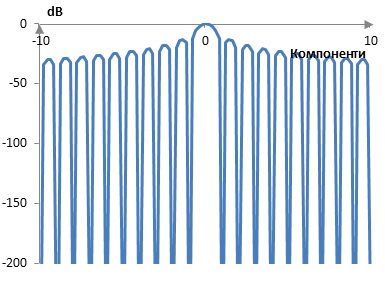
Последният компонент, който се вижда в първата графика по-горе, но е извън втората графика, има връх със стойност -53.9 dB. Спадането на страничните лобове на правоъгълния прозорец тогава е -53.9 / log2(250) = -6 dB / октава или -53.9 / log10(250) = -20 dB / декада.
Спадане на страничните лобове за често срещани прозорци
Следното е спадането на страничните лобове за често срещани прозорци (в dB за октава, dB за декада, с определенията на прозорците в този сайт).
| Бартлет и Хан | -12.7, -42.3 |
| Блекмън Точен Блекмън Обобщен Блекмън α = 0.05 α = 0.20 α = 0.35 |
-21.6, -71.7 -10.0, -33.3 -20.9, -69.5 |
| Блекмън и Харис | -14.4, -48.0 |
| Блекмън и Нътол | -12.7, -42.2 |
| Боумън | -21.4, -71.0 |
| Долф и Чебишев ω0 = 0.1 ω0 = 0.2 ω0 = 0.3 |
-7.1, -23.5 -7.1, -23.5 -7.1, -23.5 |
| Плосък | -12.1, -40.1 |
| Гаус σ = 0.3 σ = 0.5 σ = 0.7 Приблизителен ограничен на Гаус σ = 0.3 σ = 0.5 σ = 0.7 Обобщен нормален α = 2 α = 4 α = 6 |
-10.5, -34.8 -7.5, -24.8 -6.7, -22.3 -18.4, -61.1 -7.5, -24.8 |
| Хеминг | -7.9, -26.1 |
| Хан | -20.7, -68.9 |
| Хан и Поасон α = 0.3 α = 0.5 α = 0.7 |
-17.4, -57.7 -16.8, -55.9 -16.4, -54.6 |
| Кайзер α = 0.5 α = 1.0 α = 5.0 |
-6.4, -21.2 -7.3, -24.2 -15.5, -51.6 |
| Кайзер и Бесел | -11.8, -39.3 |
| Ланцош | -11.5, -38.3 |
| Нътол | -23.4, -77.6 |
| Парзън | -7.0, -23.3 |
| Клин на Планк ε = 0.2 ε = 0.4 ε = 0.5 |
-27.4, -90.9 -30.9, -102.6 -30.8, -102.3 |
| Поасон α = 0.2 α = 0.5 α = 0.8 |
-6.1, -20.3 -6.3, -20.8 -6.4, -21.4 |
| Степен на косинуса α = 1.0 α = 2.0 α = 3.0 |
-11.2, -37.1 -20.7, -68.9 -21.3, -70.6 |
| Правоъгълен | -6.0, -20.0 |
| Синусоиден | -11.2, -37.1 |
| Триъгълен | -11.4, -37.7 |
| Тъки α = 0.3 α = 0.5 α = 0.7 |
-16.3, -54.3 -15.8, -52.6 -15.3, -50.9 |
| Ултрасферичен (x0 = 1) μ = 2 μ = 3 μ = 4 |
-10.7, -35.4 -14.6, -48.6 -18.2, -60.5 |
| Уелч | -11.0, -36.5 |
Добави нов коментар