Нивото на най-високия страничен лоб на един прозорец е височината на най-високия лоб (страничен лоб, с изключение на главния лоб) на преобразуването на Фурие на прозореца.
Следното е средата на преобразуването на Фурие от 500 компонента на правоъгълния прозорец.
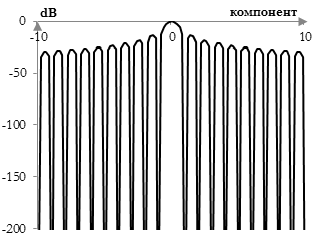
С изключение на главния лоб в средата, най-високите странични лобове са двата лоба до средния. Тяхната височина е -13.3 dB. Така, нивото на най-високия страничен лоб на правоъгълния прозорец е приблизително -13.3 dB.
Мотивация за измерването на най-високия страничен лоб
Според теоремата за конволюцията, преобразуването на Фурие на две умножени функции е умножението на преобразуванията на Фурие на двете функции. Така, прилагането на един прозорец върху един филтър е еквивалентно на използването на амплитудния спектър на прозореца като филтър върху амплитудния спектър на филтъра. Колкото по-малко (по-голямо отрицателно) е нивото на най-високия страничен лоб, толкова повече преобразуването на Фурие ще прилича на един импулс (в зависимост от размера на главния лоб), и толкова повече амплитудния спектър на прозореца ще действа върху амплитудния спектър на филтъра както един всичкопропускащ филтър и ще дава по-малки промени.
Примери на най-високия страничен лоб
Забележи, че най-високият страничен лоб не е винаги този до главния лоб. Следната графика показва главния лоб и три от страничните лобове на прозореца на Гаус (σ = 0.5).
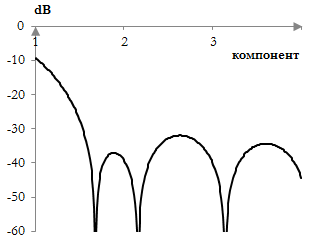
Най-високият страничен лоб е вторият страничен лоб, а не този до главния лоб.
В някои случаи, терминът ниво на най-високия страничен лоб е труден за тълкуване. Когато честотата ω0 на прозореца на Долф и Чебишев се увеличава, страничните лобове на дискретизираното преобразуване на Фурие на прозореца бавно стават плоски и следващия страничен лоб става най-висок. Следното е един от страничните лобове на един примерен прозорец на Долф и Чебишев (ω0 = 0.2).
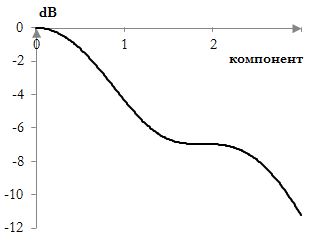
Ниво на най-високия страничен лоб за често срещани прозорци
Следното са нивата на най-високите странични лобове за често срещани прозорци (в dB, с определенията на прозорците в този сайт).
| Бартлет и Хан | -35.9 |
| Блекмън Точен Блекмън Обобщен Блекмън α = 0.05 α = 0.20 α = 0.35 |
-58.1 -68.7 -37.3 |
| Блекмън и Харис | -92.0 |
| Блекмън и Нътол | -98.3 |
| Боумън | -46.0 |
| Долф и Чебишев ω0 = 0.1 ω0 = 0.2 ω0 = 0.3 |
-29.6 -31.9 -35.1 |
| Плосък | -93.6 |
| Гаус σ = 0.3 σ = 0.5 σ = 0.7 Приблизителен ограничен на Гаус σ = 0.3 σ = 0.5 σ = 0.7 Обобщен нормален α = 2 α = 4 α = 6 |
-64.3 -32.0 -20.9 -63.6 -32.0 |
| Хеминг | -44.4 |
| Хан | -31.5 |
| Хан и Поасон α = 0.3 α = 0.5 α = 0.7 |
-37.6 -35.2 -33.0 |
| Кайзер α = 0.5 α = 1.0 α = 5.0 |
-16.6 -24.6 -38.6 |
| Кайзер и Бесел | -65.3 |
| Ланцош | -26.4 |
| Нътол | -93.3 |
| Парзън | -24.0 |
| Клин на Планк ε = 0.2 ε = 0.4 ε = 0.5 |
-13.9 -17.5 -23.2 |
| Поасон α = 0.2 α = 0.5 α = 0.8 |
-14.7 -17.5 -19.9 |
| Степен на косинуса α = 1.0 α = 2.0 α = 3.0 |
-23.0 -31.5 -39.3 |
| Правоъгълен | -13.3 |
| Синусоиден | -23.0 |
| Триъгълен | -26.5 |
| Тъки α = 0.3 α = 0.5 α = 0.7 |
-18.2 -15.1 -13.8 |
| Ултрасферичен (x0 = 1) μ = 2 μ = 3 μ = 4 |
-21.3 -27.7 -33.3 |
| Уелч | -21.3 |
Добави нов коментар