Коефициентите на прозореца на Кайзер се дават от формулата
$$a(k)=\frac{I_0(\pi\,\alpha \sqrt{1-(\frac{2k}{N-1}-1)^2}\,)}{I_0(\pi\,\alpha)}$$
където N е дължината на филтъра, k = 0, 1, …, N – 1, α е някакво реално число и I0 е нулевия ред на модифицираната функция на Бесел от първи разряд.
Изчисляване на прозореца на Кайзер
Модифицираната функция на Бесел от първи разряд (хиперболичната функция на Бесел) е следната.
$$I_{\beta}(x)=\sum_{n=0}^{\infty}\frac{1}{n!\,\Gamma(n+\beta+1)}(\frac{x}{2})^{2n+\beta}$$
където β е реда на функцията и Γ е обобщения факториал.
Забележете, че за всяко положително цяло число n, Γ(n) = (n – 1)!. Тогава, при β = 0, Γ(n + β + 1) = (n + 0 + 1 – 1)! = n!. Това означава, че модифицираната функция на Бесел от първи разряд и нулев ред е просто
$$I_0(x)=\sum_{n=0}^{\infty}(\frac{1}{n!})^2(\frac{x}{2})^{2n}$$
Тъй като сумата по-горе е ограничена и клони към крайна стойност, тя може да се изчисли приблизително за всяко x, като се вземат само първите няколко аргументи, като например
$$I_0(x)=\sum_{n=0}^{M}(\frac{1}{n!})^2(\frac{x}{2})^{2n}$$
Самият прозорец на Кайзер, ако изпишем числителя и знаменателя както по-горе, може да се изчисли по следния начин.
$$a(k)=\frac{\sum_{n=0}^{\infty}(\frac{1}{n!})^2(\frac{\pi\, \alpha \sqrt{1-(\frac{2k}{N-1}-1)^2}}{2})^{2n}}{\sum_{n=0}^{\infty}(\frac{1}{n!})^2(\frac{\pi\, \alpha}{2})^{2n}}$$
Както преди, двете суми клонят към крайна стойност и могат да се изчислят приблизително, като се вземат само първите няколко аргумента.
Пример за прозореца на Кайзер
Вземи например един нискочестотен филтър с краен импулсен спектър (FIR) и с дължина N = 201. Следното е прозореца на Кайзер при α = 3 и M = 4.
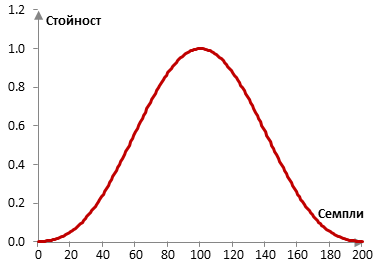
Ако пробната честота е 2000 Hz и преходната честота на филтъра е 40 Hz, тогава импулсният спектър на филтъра с правоъгълен прозорец (без прозорец) и с прозореца на Кайзер е следният.
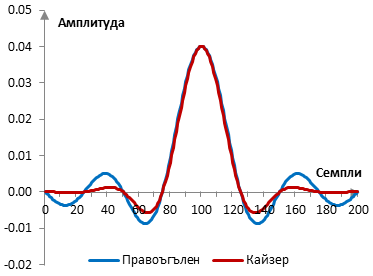
Амплитудният спектър на същия филтър е показан в графиката по-долу.
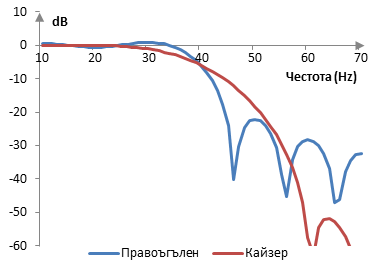
Когато |α| се увеличава, филтърът има широка преходна лента, но по-добра атенюация в лентата на спиране. Когато |α| намалява, филтърът има по-тясна преходна лента, но по-лоша атенюация. Когато α = 0, прозорецът на Кайзер става правоъгълен прозорец.
Прозорецът на Кайзер при N = 201 и при три различни стойности на α (0.5, 1 и 5) е показан в следната графика.
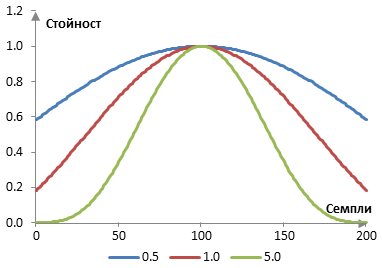
Следната графика показва амплитудните спектри на тези прозорци, при филтъра с преходна честота 40 Hz и при пробна честота 2000 Hz.
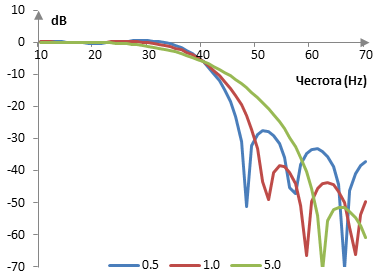
Измерения за прозореца на Кайзер
Следната графика сравнява дискретизираното преобразуване на Фурие на прозореца на Кайзер (α = 1.0) и на правоъгълния прозорец.
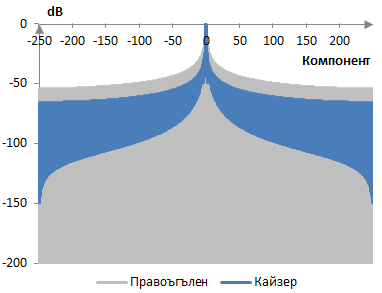
Следното са измеренията на прозореца на Кайзер.
| α | 0.5 | 1.0 | 5.0 |
| Кохерентна амплитуда | 0.85 | 0.67 | 0.42 |
| Еквивалентна лента на шума | 1.02 | 1.15 | 1.76 |
| Загуба при преработката | -0.10 dB | -0.62 dB | -2.44 dB |
| Загуба на лоба | -3.31 dB | -2.42 dB | -1.05 dB |
| Загуба при преработката в най-лошия случай | -3.41 dB | -3.04 dB | -3.49 dB |
| Ниво на най-високия страничен лоб | -16.6 dB | -24.6 dB | -38.6 dB |
| Спадане на страничните лобове | -6.4 dB / октава, -21.2 dB / декада | -7.3 dB / октава, -24.2 dB / декада | -15.5 dB / октава, -51.6 dB / декада |
| Главният лоб е -3 dB | 0.96 компонента | 1.10 компонента | 1.68 компонента |
| Главният лоб е -6 dB | 1.30 компонента | 1.52 компонента | 2.34 компонента |
| Корелация при застъпването при застъпване от 50% | 0.479 | 0.370 | 0.080 |
| Амплитудна гладкост при застъпване от 50% | 0.895 | 0.829 | 0.691 |
| Корелация при застъпването при застъпване от 75% | 0.794 | 0.783 | 0.559 |
| Амплитудна гладкост при застъпване от 75% | 0.974 | 0.958 | 0.991 |
Виж също:
Прозорец
Добави нов коментар