Коефициентите на прозореца на Боумън се дават от формулата
$$w(k)=(1-|\frac{k}{M}-1|)\,\cos(\pi |\frac{k}{M}-1|)+\frac{1}{\pi}\,\sin(\pi |\frac{k}{M}-1|)$$
където N е дължината на филтъра, M = (N – 1) / 2 и k = 0, 1, …, N – 1.
Прозорецът на Боумън е конволюцията на синусоидния прозорец със себе си.
Пример на прозореца на Боумън
Вземи един нискочестотен филтър с дължина N = 201. Следното е прозореца на Боумън.
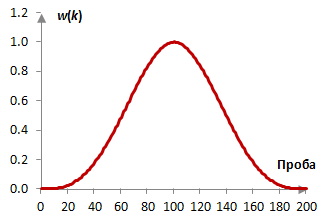
Ако пробната честота е 2000 Hz и преходната честота на филтъра е 40 Hz, тогава импулсният спектър на филтъра с правоъгълния прозорец (без прозорец) и с прозореца на Боумън е следния.
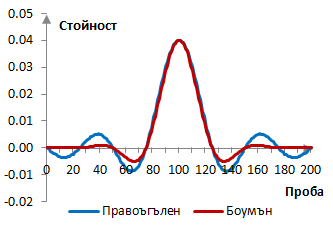
Амплитудният спектър на същия филтър е показан в графиката по-долу.
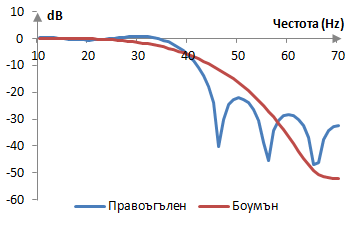
Измерения за прозореца на Боумън
Следната графика показва дискретизираното Преобразуване на Фурие на прозореца на Боумън върху дискретизираното преобразуване на Фурие на правоъгълния прозорец.
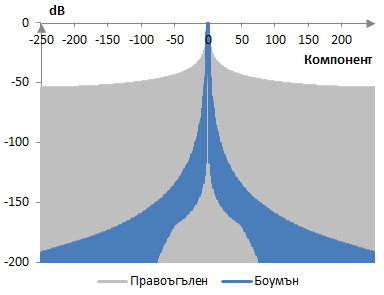
Измеренията за прозореца на Боумън са следните.
| Кохерентна амплитуда | 0.40 |
| Еквивалентна лента на шума | 1.79 |
| Загуба при преработката | -2.53 dB |
| Загуба на лоба | -1.02 dB |
| Загуба при преработката в най-лошия случай | -3.55 dB |
| Ниво на най-високия страничен лоб | -46.0 dB |
| Спадане на страничните лобове | -21.4 dB / октава, -71.0 dB / декада |
| Главният лоб е -3 dB | 1.70 компонента |
| Главният лоб е -6 dB | 2.38 компонента |
| Корелация при застъпването при застъпване от 50% | 0.073 |
| Амплитудна гладкост при застъпване от 50% | 0.637 |
| Корелация при застъпването при застъпване от 75% | 0.544 |
| Амплитудна гладкост при застъпване от 75% | 0.982 |
Виж също:
Прозорец
Добави нов коментар