Коефициентите на прозореца на Гаус се дават от формулата
$$a(k)=e^{-0.5 (\frac{k-M}{\sigma \, M})^2}$$
където N е дължината на филтъра, M = (N – 1) / 2, k = 0, 1, …, N – 1, и σ > 0.
Един примерен прозорец на Гаус
Вземи например един нискочестотен филтър с ограничен импулсен спектър (FIR) и с дължина N = 201. Следната графика показва прозореца на Гаус при σ = 0.5.
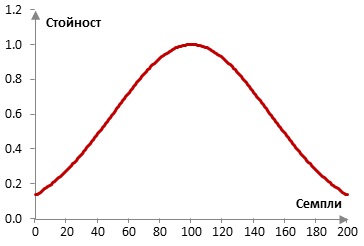
Ако пробната честота е 2000 Hz и преходната честота на филтъра е 40 Hz, тогава импулсният спектър на филтъра с правоъгълен прозорец (без прозорец) и с прозореца на Гаус е както следва.
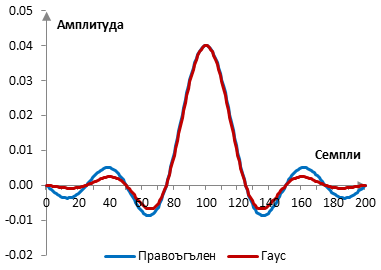
Амплитудният спектър на същия филтър е показан в графиката по-долу.
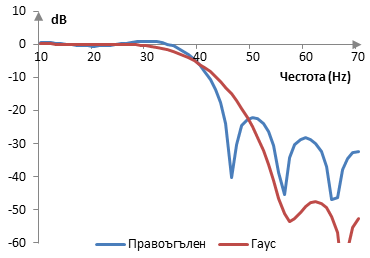
При по-големи стойности на σ, преходната лента на филтъра и разликата между амплитудите в лентата на пропускане и в лентата на спиране намаляват (преходната лента е по-малка, но атенюацията е по-лоша). Когато стойността на σ става безкрайно голяма (клони към безкрайност), прозореца на Гаус се приближава към правоъгълния прозорец. Ако пък σ клони към нула, прозореца на Гаус клони към един всичкопропускащ филтър.
Следната графика показва прозореца на Гаус при N = 201 за три различни стойности на σ (0.3, 0.5, и 0.7).
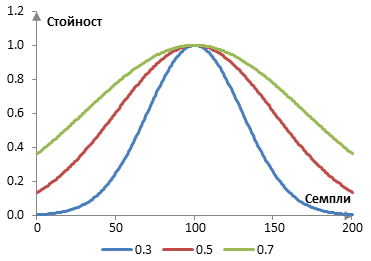
Амплитудният спектър на филтъра при тези стойности на σ, ако пробната честота е 2000 Hz и преходната честота е 40 Hz, е показан по-долу.
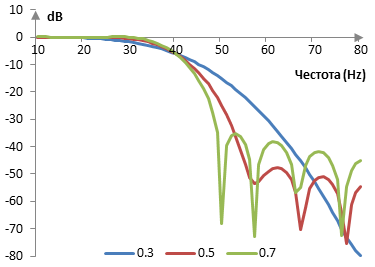
Измерения за прозореца на Гаус
Следната графика показва дискретизираното преобразуване на Фурие на прозореца на Гаус със σ = 0.3 върху дискретизираното преобразуване на Фурие на правоъгълния прозорец.

Измеренията за прозореца на Гаус са следните.
| σ | 0.3 | 0.5 | 0.7 |
| Кохерентна амплитуда | 0.37 | 0.60 | 0.74 |
| Еквивалентна лента на шума | 1.89 | 1.23 | 1.08 |
| Загуба при преработката | -2.76 dB | -0.91 dB | -0.32 dB |
| Загуба на лоба | -0.95 dB | -2.12 dB | -2.84 dB |
| Загуба при преработката в най-лошия случай | -3.71 dB | -3.04 dB | -3.16 dB |
| Ниво на най-високия страничен лоб | -64.3 dB | -32.0 dB | -20.9 dB |
| Спадане на страничните лобове | -10.5 dB / октава, -34.8 dB / декада | -7.5 dB / октава, -24.8 dB / декада | -6.7 dB / октава, -22.3 dB / декада |
| Главният лоб е -3 dB | 1.78 компонента | 1.18 компонента | 1.02 компонента |
| Главният лоб е is -6 dB | 2.50 компонента | 1.64 компонента | 1.42 компонента |
| Корелация при застъпването при застъпване от 50% | 0.060 | 0.311 | 0.431 |
| Амплитудна гладкост при застъпване от 50% | 0.497 | 0.936 | 0.878 |
| Корелация при застъпването при застъпване от 75% | 0.498 | 0.755 | 0.801 |
| Амплитудна гладкост при застъпване от 75% | 0.998 | 0.973 | 0.969 |
Приблизителен ограничен прозорец на Гаус
Горният прозорец на Гаус всъщност е един приблизителен ограничен прозорец на Гаус. Едно по-общо приближение на втория прозорец се дава от
$$a(k)= G(k) - \frac{G(-\frac{1}{2})(G(k+N)+G(k-N))}{G(-\frac{1}{2}+N)+G(-\frac{1}{2}-N)}$$ $$G(k)=e^{-0.5 (\frac{k-M}{\sigma \, M})^2}$$
Едно сравнение между прозореца на Гаус и ограничения прозорец на Гаус за N = 201 и σ = 0.5 е показано в следната графика.
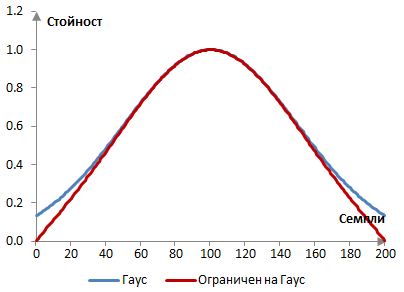
Забележи, че ограниченият прозорец на Гаус не е непременно равен на 1 в средата.
Съответните амплитудни спектри, със същия филтър, който се използва по-горе, са показани в следната графика.
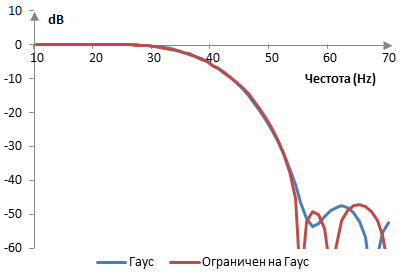
Измерения за приблизителния ограничен прозорец на Гаус
Измеренията за приблизителния ограничен прозорец на Гаус за три различни стойности на σ (0.3, 0.5 и 0.7) са следните.
| σ | 0.3 | 0.5 | 0.7 |
| Кохерентна амплитуда | 0.37 | 0.57 | 0.61 |
| Еквивалентна лента на шума | 1.89 | 1.32 | 1.24 |
| Загуба при преработката | -2.77 dB | -1.19 dB | -0.94 dB |
| Загуба на лоба | -0.95 dB | -1.85 dB | -2.07 dB |
| Загуба при преработката в най-лошия случай | -3.71 dB | -3.04 dB | -3.01 dB |
| Ниво на най-високия страничен лоб | -63.6 dB | -30.3 dB | -23.5 dB |
| Спадане на страничните лобове | -18.4 dB / октава, -61.1 dB / декада | -16.3 dB / октава, -54.3 dB / декада | -16.1 dB / октава, -53.5 dB / декада |
| Главният лоб е -3 dB | 1.78 компонента | 1.26 компонента | 1.20 компонента |
| Главният лоб е -6 dB | 2.50 компонента | 1.76 компонента | 1.64 компонента |
| Корелация при застъпването при застъпване от 50% | 0.059 | 0.261 | 0.313 |
| Амплитудна гладкост при застъпване от 50% | 0.498 | 0.841 | 0.720 |
| Корелация при застъпването при застъпване от 75% | 0.497 | 0.728 | 0.754 |
| Амплитудна гладкост при застъпване от 75% | 0.998 | 0.944 | 0.926 |
Обобщен нормален прозорец
Едно друго обобщение на прозореца на Гаус е обобщения нормален прозорец, който се дава от следната формула.
$$a(k)=e^{-0.5 |\frac{k-M}{\sigma \, M}|^{\alpha}}$$
където α > 0 (обикновено α ≥ 1). При α = 2, обобщеният нормален прозорец става прозореца на Гаус. Когато α се увеличава, върхът на прозореца става по-плосък, преходната лента на съответния филтър става по-тясна, а атенюацията му в лентата на спиране става по-лоша. Когато α клони към безкрайност, обобщеният нормален прозорец клони към правоъгълния прозорец.
Следното е обобщения нормален прозорец при три различни стойности на α (2, 4 и 6) и със σ = 0.5.
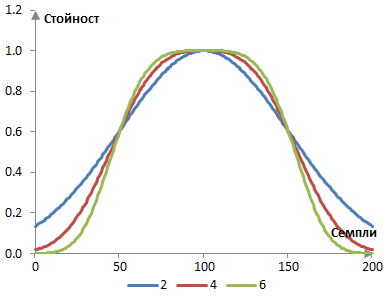
Съответните амплитудни спектри, със същия филтър който се използва по-горе, при тези прозорци, са следните.
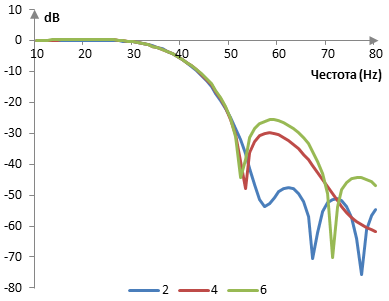
Измерения за обобщения нормален прозорец
Измеренията за обобщения нормален прозорец със σ = 0.5 и три различни стойности на α са следните.
| α | 2 | 4 | 6 |
| Кохерентна амплитуда | 0.60 | 0.54 | 0.52 |
| Еквивалентна лента на шума | 1.23 | 1.56 | 1.71 |
| Загуба при преработката | -0.91 dB | -1.94 dB | -2.34 dB |
| Загуба на лоба | -2.12 dB | -1.30 dB | -1.09 dB |
| Загуба при преработката в най-лошия случай | -3.04 dB | -3.24 dB | -3.43 dB |
| Ниво на най-високия страничен лоб | -32.0 dB | -19.7 dB | -16.3 dB |
| Спадане на страничните лобове | -7.5 dB / октава, -24.8 dB / декада | -13.2 dB / октава, -44.0 dB / декада | -30.8 dB / октава, -102.4 dB / декада |
| Главният лоб е -3 dB | 1.18 компонента | 1.50 компонента | 1.62 компонента |
| Главният лоб е -6 dB | 1.64 компонента | 2.06 компонента | 2.22 компонента |
| Корелация при застъпването при застъпване от 50% | 0.311 | 0.143 | 0.086 |
| Амплитудна гладкост при застъпване от 50% | 0.936 | 0.825 | 0.821 |
| Корелация при застъпването при застъпване от 75% | 0.755 | 0.635 | 0.582 |
| Амплитудна гладкост при застъпване от 75% | 0.973 | 0.948 | 0.900 |
Виж също:
Прозорец, Филтър на Гаус
Добави нов коментар